Circlestarks في Vitalik الاستكشاف

العنوان الأصلي: “استكشاف Circle Starks” كتبه Vitalik Buterin ، المؤسس المشارك لـ Ethereum الذي جمعته كريس ، Techub News

فرضية فهم هذا المقال هي أنك فهمت بالفعل المبادئ الأساسية للاستشارات والستاركس.إذا لم تكن على دراية بهذا ، فمن المستحسن أن تقرأ الأجزاء القليلة الأولى من هذه المقالة لتعلم الأساسيات.

في السنوات الأخيرة ، يهدف اتجاه تصميم بروتوكول ستاركس إلى التحول إلى استخدام الحقول الأصغر.استخدمت تطبيقات إنتاج Starks الأولى في حقول 256 بت ، والتي كانت عمليات معيارية على أعداد كبيرة (مثل 21888 … 95617) ، مما جعل هذه البروتوكولات متوافقة مع التوقيعات القائمة على المنحنى الإهليلجي.ومع ذلك ، فإن هذا التصميم غير فعال نسبيًا. مطلوب فقط تسعة من وقت الحساب.لحل هذه المشكلة ، بدأت ستاركس تتحول إلى حقول أصغر: أول Goldilocks ، ثم Mersenne31 و Babybear.

يعمل هذا التحول على تحسين سرعة الإثبات ، مثل قدرة Starkware على إثبات 620،000 تجزئة Poseidon2 في الثانية على جهاز كمبيوتر محمول M3.هذا يعني أنه طالما أننا على استعداد للثقة في Poseidon2 كدالة تجزئة ، يمكننا حل المشكلة في تطوير ZK-EVM الفعالة.فكيف تعمل هذه التقنيات؟كيف يتم إنشاء هذه البراهين في الحقول الأصغر؟كيف تقارن هذه البروتوكولات بحلول مثل Binius؟ستستكشف هذه المقالة هذه التفاصيل ، مع التركيز بشكل خاص على مخطط يسمى Circle Starks (Stwo في Starkware ، Plonky3 في Polygon ، ونسختي الخاصة التي تم تنفيذها في Python) ، والتي لها خصائص فريدة متوافقة مع حقل Mersenne31.

مشاكل شائعة عند استخدام حقول الرياضيات الأصغر

عند إنشاء أدلة قائمة على التجزئة (أو أي نوع من الإثبات) ، تتمثل التقنية المهمة للغاية في التحقق بشكل غير مباشر من خصائص متعدد الحدود من خلال تدقيق نتائج تقييم الحدود في نقاط عشوائية.يمكن لهذا النهج تبسيط عملية الإثبات إلى حد كبير ، حيث أن التقييم في نقاط عشوائية عادة ما يكون أسهل بكثير من التعامل مع متعدد الحدود.

على سبيل المثال ، لنفترض أن نظام الإثبات يتطلب منك إنشاء التزام متعدد الحدود ، A ، يجب أن ترضي^3 (x) + x – a (\ omega*x) = x^n (واحد شائع جدًا في ZK -snark نوع إثبات البروتوكول).يمكن أن يطلب منك البروتوكول تحديد إحداثي عشوائي؟ثم anvert a (r) = c ، تثبت أن q = \ frac {a – c} {x – r} هو متعدد الحدود.

إذا فهمت تفاصيل البروتوكول أو الآليات الداخلية مقدمًا ، فقد تجد طرقًا لتجاوز أو كسر هذه البروتوكولات.يمكن ذكر عمليات أو طرق محددة بجانب تحقيق ذلك.على سبيل المثال ، لإرضاء معادلة A (\ omega * r) ، يمكنك تعيين A (r) إلى 0 ثم جعل خط مستقيم يمر عبر هاتين النقطتين.

لمنع هذه الهجمات ، نحتاج إلى اختيار R بعد أن يوفر المهاجم (Fiat-Shamir هي تقنية تستخدم لتعزيز أمان البروتوكول ، والتي تتجنب الهجمات من خلال تحديد معلمات معينة لقيمة تجزئة معينة. يجب أن تأتي المعلمات من كبيرة بما يكفي تعيين للتأكد من أنه لا يمكن للمهاجم التنبؤ أو تخمين هذه المعلمات ، وبالتالي تحسين أمان النظام.

في البروتوكول القائم على المنحنى الإهليلجي و Starks في فترة 2019 ، تكون هذه المشكلة بسيطة: يتم تنفيذ جميع الرياضيات بأرقام 256 بت ، حتى نتمكن من تحديد R كرقم عشوائي 256 بت حتى نتمكن من القيام بذلك الآن.ومع ذلك ، في Starks في الحقول الأصغر ، لدينا مشكلة: لا يوجد سوى حوالي ملياري قيم R محتملة للاختيار من بينها ، لذلك يحتاج المهاجم الذي يريد صياغة أدلة فقط إلى تجربة 2 مليار مرة ، على الرغم من أن عبء العمل مرتفع ، ولكن بالنسبة للمهاجم الذي يحدد ، لا يزال من الممكن القيام به!

هناك حلان لهذه المشكلة:

• إجراء فحوصات عشوائية متعددة

• الحقول الممتدة

أبسط طريقة وأكثر فاعلية لإجراء عمليات فحص عشوائية متعددة: بدلاً من التحقق من إحداثي واحد ، من الأفضل التحقق من أربعة إحداثيات عشوائية بشكل متكرر.هذا ممكن نظريًا ، ولكن هناك مشاكل في الكفاءة.إذا كنت تتعامل مع متعدد الحدود مع درجة أصغر من قيمة معينة وتشغيل على مجال بحجم معين ، يمكن للمهاجم بالفعل بناء متعدد الحدود الخبيثة التي تبدو طبيعية في هذه المواقف.لذلك ، ما إذا كان بإمكانهم كسر البروتوكول بنجاح هو سؤال احتمالي ، لذلك يجب زيادة عدد جولات الشيكات لتعزيز الأمن العام وضمان الدفاع الفعال ضد المهاجمين.

هذا يؤدي إلى حل آخر: مجال ممتد ، المجال الممتد يشبه الجمع ، لكنه يعتمد على المجالات المحدودة.نقدم قيمة جديدة ، يُشار إليها باسم α \ alphaα ، ونعلن أنها تفي بعلاقة معينة ، مثل α2 = بعض القيمة \ alpha^2 = \ text {بعض القيمة} α2 = بعض القيمة.وبهذه الطريقة ، نقوم بإنشاء بنية رياضية جديدة تتيح عمليات أكثر تعقيدًا على المجالات المحدودة.في هذا المجال الممتد ، يصبح حساب الضرب مضاعفة باستخدام القيمة الجديدة α \ alphaα.يمكننا الآن معالجة أزواج القيمة في المجالات الممتدة ، وليس فقط الأرقام الفردية.على سبيل المثال ، إذا عملنا في حقول مثل Mersenne أو BabyBear ، فإن هذا التمديد يتيح لنا الحصول على المزيد من خيارات القيمة ، وبالتالي تحسين الأمان.لزيادة حجم الحقل ، يمكننا تطبيق نفس التقنية مرارًا وتكرارًا.نظرًا لأننا استخدمنا α \ alphaα ، نحتاج إلى تحديد قيمة جديدة ، والتي تظهر في Mersenne31 على أنها اختيار α \ alphaα بحيث α2 = بعض القيمة \ alpha^2 = \ text {بعض القيمة α2 = بعض القيمة.

الكود (يمكنك تحسينه مع Karatsuba)

من خلال توسيع نطاق المجال ، لدينا الآن قيم كافية لاختيار تلبية احتياجاتنا من الأمان.إذا كنت تتعامل مع متعدد الحدود بشهادة أصغر من DDD ، فيمكن أن توفر كل جولة أمانًا 104 بت.هذا يعني أن لدينا أمن كافٍ.إذا كنت بحاجة إلى الوصول إلى مستوى أمان أعلى ، مثل 128 بت ، يمكننا إضافة بعض أعمال الحوسبة الإضافية إلى البروتوكول لتعزيز الأمان.

يتم استخدام المجالات الممتدة فقط في بروتوكول FRI (Fast Reed-Solomon Interactive) والسيناريوهات الأخرى التي تتطلب مجموعات خطية عشوائية.لا تزال معظم العمليات الرياضية يتم تنفيذها على الحقول الأساسية ، والتي عادة ما تكون حقولًا هي Modulo PPP أو QQQ.وفي الوقت نفسه ، تتم جميع بيانات التجزئة تقريبًا على الحقل الأساسي ، لذلك كل قيمة فقط لها أربعة بايت.يمكن أن يستفيد القيام بذلك من كفاءة الحقول الصغيرة ، مع استخدام الحقول الكبيرة عند الحاجة إلى تحسينات الأمان.

الجمعة العادية

عند بناء Snark أو Stark ، تكون الخطوة الأولى عادةً ما تكون حساءًا.هذا هو ترجمة المشكلات الحسابية التعسفية إلى معادلة حيث تكون بعض المتغيرات والمعاملات متعددة الحدود.على وجه التحديد ، ستبدو هذه المعادلة عادةً مثل p (x ، y ، z) = 0p (x ، y ، z) = 0 ، حيث تكون p متعددة الحدود ، x ، y ، و z هي المعلمة المحددة ، ويحتاج المحلل إلى ذلك توفير قيم X و Y.بمجرد وجود مثل هذه المعادلة ، يتوافق حل المعادلة مع حل المشكلة الحسابية الأساسية.

لإثبات أن لديك حلًا ، يجب أن تثبت أن القيمة التي تقترحها هي بالفعل متعددة الحدود (بدلاً من الكسر ، أو في بعض الأماكن ، تبدو وكأنها كثير الحدود وفي أماكن أخرى متعددة الحدود ، إلخ). ، وهذه متعدد الحدود لديها درجة قصوى معينة.للقيام بذلك ، نستخدم تقنية مزيج خطي عشوائي خطوة بخطوة:

• لنفترض أن لديك قيمة تقييم متعددة الحدود ، وتريد أن تثبت أن شهادتها أقل من 2^{20}

• النظر في كثير الحدود b (x^2) = a (x) + a (-x) ، c (x^2) = \ frac {a (x)-a (-x)} {x}

• D عبارة عن مزيج خطي عشوائي من B و C ، أي D = B+RCD = B+RCD = B+RC ، حيث R هو معامل عشوائي.

في الأساس ، ما يحدث هو عزلات B حتى معاملات A ، و؟بالنظر إلى B و C ، يمكنك استعادة متعدد الحدود A: A (X) = B (X^2) + XC (X^2).إذا كانت درجة A أقل من 2^{20} ، فستكون درجات B و C هي درجات A ودرجات A ، على التوالي ، ناقص 1.لأن الجمع بين المصطلحات الزوجية والغريبة لا يزيد من الدرجة.نظرًا لأن D عبارة عن مزيج خطي عشوائي من B و C ، يجب أن تكون درجة D هي أيضًا درجة A ، والتي تتيح لك التحقق مما إذا كانت درجة A تفي بمتطلبات D.

أولاً ، يقوم FRI بتبسيط عملية التحقق من خلال تبسيط مشكلة إثبات درجة الحدود من D لمشكلة إثبات درجة متعدد الحدود لـ D/2.يمكن تكرار هذه العملية عدة مرات ، مما يؤدي إلى تبسيط المشكلة في منتصف الطريق في كل مرة.

مبدأ العمل في FRI هو تكرار هذه العملية المبسطة.على سبيل المثال ، إذا بدأت بإثبات على أن الحدود هو D ، من خلال سلسلة من الخطوات ، فسوف يثبت في النهاية أن متعدد الحدود هو D/2.بعد كل تبسيط ، يتم تقليل درجة متعدد الحدود المولدة تدريجياً.إذا لم يكن ناتج المرحلة هو الحدود الحدود المتوقعة ، فسوف تفشل هذه الجولة من الشيكات.إذا حاول شخص ما دفع متعدد الحدود ليس درجة د من خلال هذه التقنية ، ثم في الجولة الثانية من الإنتاج ، سيكون لدى الدرجة احتمال معين بأنها لن تفي بالتوقعات ، وفي الجولة الثالثة ، سيكون هناك أكثر احتمالًا أن تكون حالة غير متطابقة.يمكن أن يكتشف هذا التصميم بشكل فعال ورفض المدخلات التي لا تفي بالمتطلبات.إذا كانت مجموعة البيانات تساوي متعدد الحدود مع درجة D في معظم المواقع ، فإن مجموعة البيانات هذه لديها القدرة على التحقق من صحة FRI.ومع ذلك ، من أجل بناء مجموعة البيانات هذه ، يحتاج المهاجم إلى معرفة الحدود الفعلية ، لذلك حتى الدليل المعيب الطفيف يشير إلى أن المثل قادر على إنشاء دليل “حقيقي”.

دعونا نلقي نظرة فاحصة على ما يجري هنا والخصائص اللازمة لجعل هذا العمل.في كل خطوة ، نقوم بتقليل عدد الحدود الحدود بمقدار النصف ، مع تقليل مجموعة النقاط (مجموعة النقاط التي نركز عليها) بمقدار النصف.السابق هو مفتاح جعل بروتوكول FRI (Fast Reed-Solomon Interactive) يعمل بشكل صحيح.هذا الأخير يجعل الخوارزمية تعمل بسرعة كبيرة: نظرًا لأن مقياس كل جولة يتم تقليله بمقدار النصف مقارنة بالجولة السابقة ، فإن تكلفة الحساب الكلية هي O (n) ، وليس O (n*log (n)).

لتحقيق انخفاض تدريجي في المجال ، يتم استخدام رسم خرائط ثنائي إلى واحد ، أي يتم تعيين كل نقطة إلى واحدة من النقطتين.يتيح لنا هذا التعيين تقليل حجم مجموعة البيانات الخاصة بنا إلى النصف.ميزة مهمة لهذا التعيين ثنائي إلى واحد هي أنه قابل للتكرار.وهذا هو ، عندما نطبق هذا التعيين ، لا تزال مجموعة النتائج الناتجة تحتفظ بنفس الخصائص.لنفترض أننا نبدأ بمجموعة فرعية متعددة.هذه المجموعة الفرعية عبارة عن مجموعة S حيث تحتوي كل عنصر X على 2x متعددة في المجموعة أيضًا.إذا قمت بإجراء عملية مربعة على Set S (أي خريطة كل عنصر X في المجموعة إلى X^2) ، فإن المجموعة الجديدة S^2 تحتفظ بنفس السمات.تتيح لنا هذه العملية مواصلة تقليل حجم مجموعة البيانات حتى ننتهي بقيمة واحدة فقط.على الرغم من أنه من الناحية النظرية ، يمكننا تضييق نطاق مجموعة البيانات إلى قيمة واحدة فقط ، في الممارسة العملية ، عادة ما تتوقف قبل الوصول إلى مجموعة أصغر.

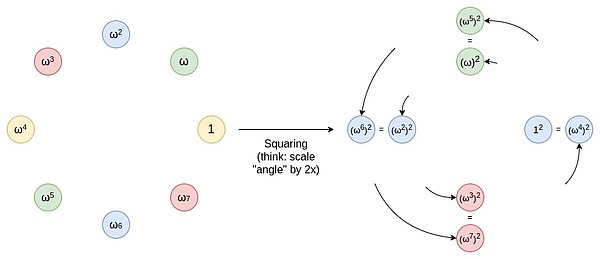
يمكنك التفكير في هذه العملية كعملية لتوسيع خط (على سبيل المثال ، شريحة أو قوس) على محيط ، مما تسبب في تدوير اثنين من المنعطفات حول المحيط.على سبيل المثال ، إذا كانت النقطة في موضع درجة X على محيط ، ثم بعد هذه العملية ، فإنها تنتقل إلى وضع درجة 2x.كل نقطة على محيط لها نقطة مقابلة عند 180 إلى 359 درجة ، وستتداخل هاتان النقطتان.هذا يعني أنه عندما تقوم بتخطيط نقطة من x إلى درجات 2x ، فإنه يتزامن مع موضع عند x+180 درجة.يمكن تكرار هذه العملية.أي أنه يمكنك تطبيق عملية التعيين هذه عدة مرات ، في كل مرة نقل النقاط على محيط موقعها الجديد.

لجعل تقنية التعيين فعالة ، يحتاج حجم المجموعة الفرعية الضاعفة الأصلية إلى الحصول على قوة كبيرة 2 كعامل.Babybear هو نظام يحتوي على معامل محدد هو معامله قيمة بحيث تحتوي المجموعة الفرعية الضاعفة القصوى على جميع القيم غير الصفرية ، وبالتالي فإن حجم المجموعة الفرعية هو 2K – 1 (حيث K هو عدد أجزاء المعامل).هذه المجموعة الفرعية ذات الحجم مناسبة للغاية للتقنية أعلاه لأنها تتيح تقليل درجة متعدد الحدود بشكل فعال من خلال تطبيق عمليات رسم الخرائط بشكل متكرر.في Babybear ، يمكنك تحديد مجموعة فرعية من الحجم 2^k (أو استخدام المجموعة بأكملها) ، ثم تطبيق طريقة FRI لتقليل درجة متعدد الحدود تدريجياً إلى 15 ، والتحقق من درجة متعدد الحدود في النهاية.تستخدم هذه الطريقة خصائص المعامل وحجم مجموعات الضرب الفرعية ، مما يجعل عملية الحساب فعالة للغاية.Mersenne31 هو نظام آخر مع معامل بعض القيمة ، بحيث يكون حجم المجموعة الفرعية الضاعفة 2^31 – 1.在这种情况下，乘法子群的大小只有一个 2 的幂作为因子，这使得它只能被除以 2 一次。لم تعد المعالجة اللاحقة تنطبق على التقنيات المذكورة أعلاه ، أي أنه من المستحيل استخدام FFT لإجراء تخفيض فعال في الحدود الحدودية مثل Babybear.

Mersenne31 域非常适合在现有的 32 位 CPU/GPU 操作中进行算术运算。بسبب خصائص المعامل الخاصة به (على سبيل المثال ، 2^{31} – 1) ، يمكن تحقيق العديد من العمليات باستخدام عمليات بت فعالة: إذا كانت نتيجة إضافة رقمين تتجاوز المعامل ، فيمكنك تحويل النتيجة من المعامل reduce to the appropriate range.عملية الإزاحة هي عملية فعالة للغاية.乘法运算中，可以使用特定的 CPU 指令（通常称为高位位移指令）来处理结果。这些指令可以高效地计算乘法的高位部分，从而提高了运算的效率。في مجال Mersenne31 ، بسبب الخصائص المذكورة أعلاه ، تكون العمليات الحسابية أسرع بنحو 1.3 مرة من مجال Babybear.يوفر Mersenne31 كفاءة حوسبة أعلى.إذا كان من الممكن تنفيذ FRI في مجال Mersenne31 ، فإن هذا سيحسن بشكل كبير من كفاءة الحوسبة ويجعل تطبيقات FRI أكثر كفاءة.

دائرة الجمعة

هذا هو ذكاء سيركل ستاركس.تتكون هذه المجموعة من جميع النقاط التي تلبي بعض الشروط المحددة ، على سبيل المثال ، X^2 Mod P تساوي مجموعة من النقاط التي تكون فيها قيمة محددة.

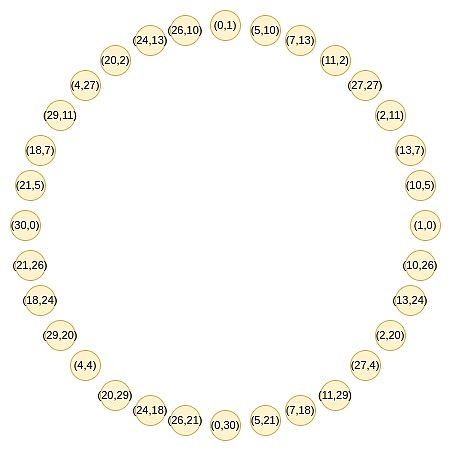
تتبع هذه النقاط قاعدة الإضافة ، والتي قد تجدها على دراية إذا كنت قد قمت بتصنيع المثلثات أو الضرب المعقد مؤخرًا.

(x_1 ، y_1) + (x_2 ، y_2) = (x_1x_2 – y_1y_2 ، x_1y_2 + x_2y_1)

الشكل المزدوج هو:

2 * (x ، y) = (2x^2 – 1 ، 2xy)

الآن ، دعونا نركز على النقاط الموجودة في الوضع الفردي في هذه الدائرة:

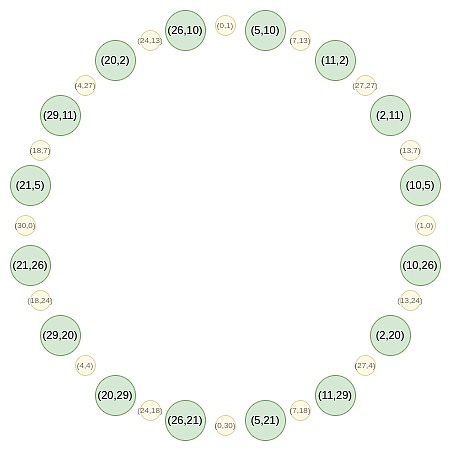
أولاً ، نتقارب جميع النقاط على خط مستقيم.我们在常规 FRI 中使用的 B (x²) 和 C (x²) 公式的等效形式是：

f_0 (x) = \ frac {f (x ، y) + f (x ، -y)} {2}

بعد ذلك ، يمكننا القيام بمجموعات خطية عشوائية للحصول على p (x) أحادي البعد ، والتي يتم تعريفها على مجموعة فرعية من الخط السيني:

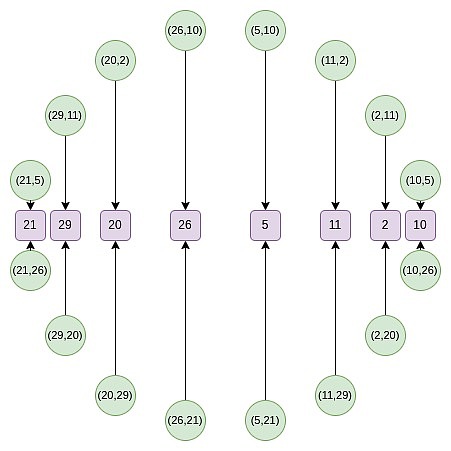
بدءًا من الجولة الثانية ، تغير التعيين:

f_0 (2x^2-1) = \ frac {f (x) + f (-x)} {2}

هذا التعيين يقلل فعليًا من حجم ما ورد أعلاه بمقدار النصف في كل مرة ، وما يحدث هنا هو أن كل X يمثل نقطتين بمعنى: (x ، y) و (x ، -y).و (x → 2x^2 – 1) هي قاعدة مضاعفة النقطة أعلاه.لذلك ، نقوم بتحويل إحداثيات X لنقطتين معاكستين على الدائرة إلى إحداثيات X للنقاط المضاعفة.

على سبيل المثال ، إذا أخذنا القيمة الثانية للرقم من يمين الدائرة على الرقم الثاني وقمنا بتطبيق التعيين 2 → 2 (2^2) – 1 = 7 ، نحصل على نتيجة 7.إذا عدنا إلى الدائرة الأصلية ، (2 ، 11) هي النقطة الثالثة من اليمين ، لذلك بعد ضربها ، نحصل على النقطة السادسة من اليمين ، أي (7 ، 13).

كان يمكن أن يتم ذلك في الفضاء ثنائي الأبعاد ، ولكن العمل في مساحة أحادية البعد سيجعل العملية أكثر كفاءة.

دائرة FFTS

الخوارزمية المرتبطة ارتباطًا وثيقًا بـ FRI هي FFT ، والتي تحول قيم التقييم n من كثير الحدود بدرجة أقل من N إلى N معاملات الحدود.تشبه عملية FFT FRI ، باستثناء أنه بدلاً من إنشاء مجموعات خطية عشوائية من F_0 و F_1 في كل خطوة ، تقوم FFT بشكل متكرر بتنفيذ FFTs نصف الحجم عليها ويأخذ إخراج FFT (F_0) كمعامل متساوي ، إخراج FFT (F_1) كمعامل غريب.

تدعم Circle Group أيضًا FFT ، والتي تم بناؤها بشكل مشابه للجمعة.ومع ذلك ، فإن الاختلاف الرئيسي هو أن الكائنات التي تتم معالجتها بواسطة Circle FFT (و Circle FRI) ليست متعددة الحدود بشكل صارم.بدلاً من ذلك ، فهي ما يسمى مسافة Riemann -Roch بشكل رياضي: في هذه الحالة ، يتم تحضير متعدد الحدود (x^2 + y^2 – 1 = 0).وهذا هو ، نتعامل مع أي مضاعف من x^2 + y^2 – 1 كصفر.هناك طريقة أخرى لفهمها هي: نسمح فقط بسلطة واحدة من y: بمجرد ظهور مصطلح y^2 ، نستبدله بـ 1 – x^2.

هذا يعني أيضًا أن إخراج المعاملات بواسطة الدائرة FFT ليست أحادية الجمعة العادية (على سبيل المثال ، إذا كان إخراج FRI العادي [6 ، 2 ، 8 ، 3] ، فإننا نعلم أن هذا يعني p (x) = 3x^ 3 + 8x^2 + 2x + 6).بدلاً من ذلك ، فإن معاملات الدائرة fft هي أساس الدائرة fft: {1 ، y ، x ، xy ، 2x^2 – 1 ، 2x^2y – y ، 2x^3 – x ، 2x^3y – xy ، 8x^4 – 8x^2 + 1 …}

والخبر السار هو أنه كمطور ، يمكنك تجاهل هذا تمامًا تقريبًا.لا تتطلب منك Starks معرفة المعاملات.بدلاً من ذلك ، يمكنك ببساطة تخزين الحدود كمجموعة من قيم التقييم في مجال معين.المكان الوحيد لاستخدام FFT هو تنفيذ (على غرار مساحة Riemann-Roch) التوسع المنخفض من الدرجة المنخفضة: مع إعطاء القيم n ، قم بإنشاء قيم k*n ، كل ذلك على نفس الحدود.في هذه الحالة ، يمكنك استخدام FFT لإنشاء معاملات ، إلحاق (K-1) n Zeros بهذه المعاملات ، ثم استخدام FFT العكسي للحصول على مجموعة أكبر من قيم التقييم.

Circle FFT ليس هو نوع FFT الخاص الوحيد.تعتبر FFTs المنحنية الإهليلجية أكثر قوة لأنها يمكن أن تعمل على أي مجال محدود (المجال الرئيسي ، المجال الثنائي ، إلخ).ومع ذلك ، فإن ECFFT أكثر تعقيدًا وغير فعال ، لذا نظرًا لأننا يمكننا استخدام Circle FFT على p = 2^{31} -1 ، اخترنا استخدامه.

من هنا ، نتعمق في بعض التفاصيل الغامضة ، وتختلف تفاصيل تنفيذ تنفيذ Circle Starks عن تلك الخاصة بـ Starks العادية.

حاصل

في بروتوكول Stark ، تتمثل العملية الشائعة في إجراء عمليات الحاصل على نقاط محددة ، والتي يمكن اختيارها عن قصد أو عشوائي.على سبيل المثال ، إذا كنت تريد إثبات أن p (x) = y ، يمكنك القيام بذلك بواسطة:

حوسبة الحوسبة: بالنظر إلى متعدد الحدود P (x) و y الثابت ، الحوسبة quient q = {p – y}/{x – x} ، حيث x هي النقطة المحددة.

إثبات الحدود: إثبات Q هو متعدد الحدود ، وليس قيمة كسرية.وبهذه الطريقة ، ثبت أن p (x) = y صحيح.

بالإضافة إلى ذلك ، في بروتوكول Deep-PRI ، يتمثل الاختيار العشوائي لنقاط التقييم في تقليل عدد فروع Merkle ، وبالتالي تحسين أمن بروتوكول FRI وكفاءته.

عند التعامل مع البروتوكول الصارخ لمجموعة الدائرة ، نظرًا لعدم وجود وظيفة خطية يمكن تمريرها عبر نقطة واحدة ، يجب استخدام تقنيات مختلفة لاستبدال طريقة تشغيل الحاصل التقليدية.يتطلب هذا عادة تصميم خوارزميات جديدة باستخدام الخصائص الهندسية الفريدة لمجموعة الدائرة.

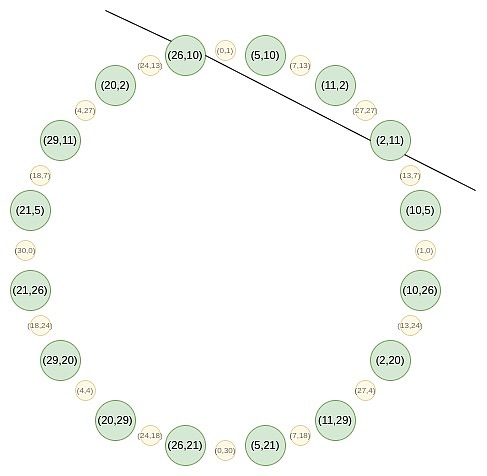
في مجموعة الدائرة ، يمكنك إنشاء وظيفة الظل إلى الظل في نقطة (p_x ، p_y) ، ولكن هذه الوظيفة سيكون لها عدد ثقيل من 2 إلى هذه النقطة ، أي لجعل متعدد الحدود مضاعفًا لوظيفة خطية ، والتي يجب أن ترضي حالة أكثر صرامة من كونها صفر فقط في تلك المرحلة.لذلك ، لا يمكنك إثبات نتائج التقييم عند نقطة واحدة.فكيف يجب أن نتعامل معها؟

كان علينا أن نواجه هذا التحدي ، الذي أثبتته من خلال تقييمه بنقطتين ، وبالتالي إضافة نقطة افتراضية لا نحتاج إلى التركيز عليها.

وظيفة الخط: AX + بواسطة + ج.إذا قمت بتحويلها إلى معادلة وأجبرتها على تساوي 0 ، فيمكنك التعرف عليها كخط في ما يسمى شكلًا قياسيًا في الرياضيات في المدرسة الثانوية.

إذا كان لدينا polynomial p يساوي Y_1 في x_1 و y_2 في x_2 ، يمكننا اختيار وظيفة الاستيفاء l ، والتي تساوي y_1 في x_1 و y_2 في x_2.يمكن التعبير عن ذلك ببساطة على أنه l = \ frac {y_2 – y_1} {x_2 – x_1} \ cdot (x – x_1) + y_1.

ثم نثبت أن p يساوي y_1 في x_1 و y_2 عند x_2 ، عن طريق طرح l (بحيث يكون p – l صفرًا عند كلتا النقطتين) ، و L (أي وظيفة خطية بين x_2 – x_1) مقسومًا على l إلى l إثبات أن الحاصل Q هو متعدد الحدود.

التلاشي متعدد الحدود

في Stark ، المعادلة الحية التي تحاول إثباتها عادة ما تشبه C (p (x) ، p ({next} (x))) = z (x) ⋅ h (x) ، حيث z (x) هو متعدد الحدود يساوي الصفر خلال مجال التقييم الأصلي.في Stark العادية ، هذه الوظيفة هي x^n – 1.في صارخ دائري ، الوظيفة المقابلة هي:

Z_1 (x ، y) = y

Z_2 (x ، y) = x

z_ {n+1} (x ، y) = (2 * z_n (x ، y)^2) – 1

لاحظ أنه يمكنك استنتاج كثير الحدود المختفي من وظيفة الانهيار: في Stark Stark العادية ، تقوم بإعادة استخدام X → X^2 ، بينما في Stark دائرية يمكنك إعادة استخدام X → 2x^2 – 1.ومع ذلك ، في الجولة الأولى ، ستقوم بعلاجات مختلفة لأن الجولة الأولى خاصة.

ترتيب بت عكسي

في Starks ، عادة ما لا يتم ترتيب تقييم متعدد الحدود بالترتيب “الطبيعي” (على سبيل المثال ، P (ω) ، P (ω2) ، … :

p (\ omega^{\ frac {3n} {8}})

إذا قمنا بتعيين n = 16 وركزنا فقط على صلاحيات ω التي نقوم بتقييمها ، فإن القائمة تبدو مثل:

{0 ، 8 ، 4 ، 12 ، 2 ، 10 ، 6 ، 14 ، 1 ، 9 ، 5 ، 13 ، 3 ، 11 ، 7 ، 15}

يحتوي هذا النوع على خاصية أساسية يتم تجميعها معًا في وقت مبكر من تقييم FRI ستكون متاخمة في هذا النوع.على سبيل المثال ، الخطوة الأولى لمجموعات FRI X و -X.في حالة n = 16 ، ω^8 = -1 ، مما يعني p (ω^i)) و (p (-Ω^i) = p (ω^{i+8}) \).正如我们所见，这些正是紧挨在一起的对。FRI 的第二步将 P (ω^i) 、 P (ω^{i+4}) 、P (ω^{i+8}) 和 P (ω^{i+12}) 分组。这些正是我们看到的四个一组的情况，以此类推。إن القيام بذلك يجعل FRI أكثر توفيرًا للمساحة لأنه يتيح لك تقديم دليل على Merkle للقيم المطبقة معًا (أو ، إذا قمت بطي عجلات K في وقت واحد ، كل قيم 2^K).

في Circle Starks ، يختلف بنية الطية قليلاً: في الخطوة الأولى ، نربط (x ، y) مع (x ، y) ؛ q  , select p and  q so that Q^i (p) = -Q^i (q), where Q^i is a mapping repeated x → 2x^2-1  i times.إذا نظرنا إلى هذه النقاط من الموضع على الدائرة ، فحينئذٍ في كل خطوة ، يبدو أن هذه النقطة الأولى مقترنة بالنقطة الأخيرة ، والنقطة الثانية مقترنة بالنقطة قبل الأخيرة ، وما إلى ذلك.

为了调整反向位序以反映这种折叠结构，我们需要反转除了最后一位的每一位。我们保留最后一位，并用它来决定是否翻转其他位。

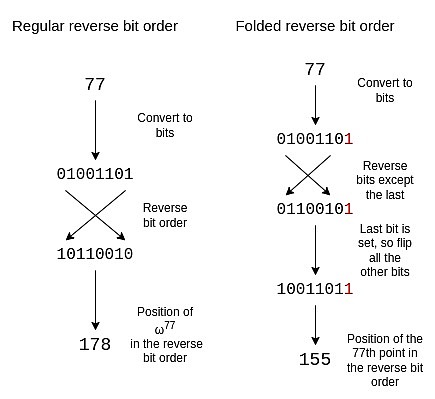
一个大小为 16 的折叠反向位序如下：

{0 ، 15 ، 8 ، 7 ، 4 ، 11 ، 12 ، 3 ، 2 ، 13 ، 10 ، 5 ، 6 ، 9 ، 14 ، 1}

إذا لاحظت الدائرة في القسم السابق ، فستجد أن النقاط 0 و 15 و 8 و 7 (عكس اتجاه عقارب الساعة من اليمين) هي (x ، y) ، (x ، -y) ، (-x ، – – y) و (-x ، y) النماذج ، وهي بالضبط ما نحتاجه.

كفاءة

هذه البروتوكولات فعالة للغاية في سيركل ستاركس (وعموما starks برئيس 31 بت).عادةً ما يتضمن الحساب الذي ثبت في الدائرة Stark عدة أنواع من الحسابات:

1. الحساب الأصلي: يستخدم لمنطق الأعمال ، مثل العد.

2. الحساب الأصلي: يستخدم في التشفير ، مثل وظائف التجزئة مثل Poseidon.

3. ابحث عن المعلمات: طريقة حساب عامة وفعالة تنفذ حسابات مختلفة عن طريق قراءة القيم من الجداول.

المقياس الرئيسي للكفاءة هو: في الحوسبة ، هل يمكنك الاستفادة القصوى من المساحة بأكملها للعمل المفيد أو تترك الكثير من المساحة الحرة.في الزخ – عادة ما يكون هناك الكثير من المساحة الحرة: عادة ما تتضمن جداول العمل والبحث عن حسابات للأعداد الصغيرة (غالبًا ما تكون هذه الأرقام أقل من N ، N هي العدد الإجمالي لخطوات الحساب ، وبالتالي أقل من 2^ {25 في الممارسة}) ، لكن لا تزال بحاجة إلى دفع تكلفة استخدام حقل بت من الحجم 2^{256}.هنا ، حجم الحقل هو 2^{31} ، وبالتالي فإن المساحة الضائعة ليست كثيرًا.تجزئة التعقيد المنخفضة الحسابية المصممة للقطاعات (مثل Poseidon) تستفيد أقصى استفادة من كل جزء من كل رقم في التتبع في أي حقل.

يعد Binius حلاً أفضل من Circle Starks لأنه يتيح لك مزج الحقول ذات الأحجام المختلفة لتعبئة بت أكثر كفاءة.يوفر Binius أيضًا خيار إجراء إضافة 32 بت دون زيادة سماعة جدول البحث.ومع ذلك ، فإن سعر هذه المزايا (في رأيي) هو أنها ستجعل المفهوم أكثر تعقيدًا ، في حين أن Circle Starks (و starks العادية القائمة على Babybear) بسيطة نسبيًا من الناحية المفاهيمية.

الخلاصة: رأيي في Circle Starks

دائرة ستاركس لا شيء أكثر تعقيدًا للمطورين من ستاركس.أثناء عملية التنفيذ ، فإن الأسئلة الثلاثة المذكورة أعلاه هي الفرق في الإجهازية التقليدية.على الرغم من أن الرياضيات التي تقف وراء الحدود التي تديرها Circle FRI معقدة للغاية ويستغرق بعض الوقت لفهمها وتقديرها ، فإن هذا التعقيد مخفي في الواقع بشكل أقل وضوحًا ولن يشعر المطورون به مباشرة.

يمكن أن يكون فهم دائرة الجمعة و Circle FFTS وسيلة لفهم FFTs الخاصة الأخرى: أبرزها هي FFTs المجال الثنائي ، مثل FFTS المستخدمة من قبل Binius و Libstark السابقة ، وبعض التركيبات الأكثر تعقيدًا ، مثل المنحنى الإهليلجي ، هذه ، هذه يمكن دمج FFTS باستخدام رسم خرائط أقل إلى حد ما مع عملية منحنى الإهليلجي.

الجمع بين Mersenne31 ، Babybear ، وتقنيات المجال الثنائي مثل Binius ، نشعر أننا نقترب من حدود الكفاءة في الطبقة الأساسية من Starks.في هذه المرحلة ، أتوقع أن يكون لاتجاه تحسين Stark النقاط الرئيسية التالية:

الحساب لزيادة كفاءة وظائف التجزئة والتوقيعات: تحسين بدائل التشفير الأساسية مثل وظائف التجزئة والتوقيعات الرقمية في الشكل الأكثر كفاءة ، بحيث يمكنها تحقيق الأداء الأمثل عند استخدامها في أدلة صارخة.وهذا يعني تحسينات خاصة لهذه البدائية لتقليل الجهد الحسابي وزيادة الكفاءة.

أداء البناء العودية لتمكين المزيد من التوازي: يشير البناء العودية إلى التطبيق العودية لعملية الإثبات الصارخ إلى مستويات مختلفة ، وبالتالي تحسين قوة المعالجة الموازية.وبهذه الطريقة ، يمكن استخدام موارد الحوسبة بشكل أكثر كفاءة ويمكن تسريع عملية الإثبات.

الأجهزة الافتراضية الحسابية لتحسين تجربة المطور: المعالجة الحسابية للأجهزة الافتراضية تجعل الأمر أكثر كفاءة وبساطة للمطورين لإنشاء وتشغيل مهام الحوسبة.يتضمن ذلك تحسين الأجهزة الافتراضية لسهولة الاستخدام في البراهين الصارخة ، وتحسين تجربة المطورين عند بناء واختبار العقود الذكية أو مهام الحوسبة الأخرى.