
Titre original: « Exploring Circle Starks » écrit par Vitalik Buterin, co-fondateur Ethereum compilé par Chris, Techub News
La prémisse de compréhension de cet article est que vous avez déjà compris les principes de base des pièges et des étoiles.Si vous n’êtes pas familier avec cela, il est recommandé de lire les premières parties de cet article pour apprendre les bases.
Ces dernières années, la tendance de la conception du protocole Starks est de passer à l’utilisation de champs plus petits.Les premières implémentations de production de Starks ont utilisé des champs 256 bits, qui étaient des opérations modulaires sur un grand nombre (comme 21888 … 95617), ce qui rendait ces protocoles compatibles avec les signatures basées sur la courbe elliptique.Cependant, cette conception est relativement inefficace. Un neuvième seulement du temps de calcul est nécessaire.Pour résoudre ce problème, Starks a commencé à se tourner vers des champs plus petits: d’abord Goldilocks, puis Mersenne31 et Babybear.
Ce changement améliore la vitesse de preuve, comme la capacité de Starkware à prouver 620 000 hachages Poseidon2 par seconde sur un ordinateur portable M3.Cela signifie que tant que nous sommes prêts à faire confiance à Poséidon2 en tant que fonction de hachage, nous pouvons résoudre le problème dans le développement de ZK-EVM efficace.Alors, comment fonctionnent ces technologies?Comment ces preuves sont-elles établies sur des champs plus petits?Comment ces protocoles se comparent-ils à des solutions comme Binius?Cet article explorera ces détails, se concentrant spécifiquement sur un schéma appelé Circle Starks (STWO dans Starkware, Plonky3 dans Polygon, et ma propre version implémentée dans Python), qui a des propriétés uniques compatibles avec le champ Mersenne31.
Problèmes courants lors de l’utilisation de petits champs mathématiques
Lors de la création de preuves basées sur le hachage (ou de tout type de preuve), une technique très importante consiste à vérifier indirectement les propriétés des polynômes en éprouvant les résultats de l’évaluation des polynômes à des points aléatoires.Cette approche peut considérablement simplifier le processus de preuve, car l’évaluation à des points aléatoires est généralement beaucoup plus facile que de gérer l’ensemble du polynôme.
Par exemple, supposons qu’un système de preuve vous oblige à générer un engagement pour les polynômes, a, doit satisfaire un ^ 3 (x) + x – a (\ omega * x) = x ^ n (très courant dans le zk-snark Type de preuve de protocole).Le protocole peut vous demander de sélectionner une coordonnée aléatoire?Ensuite, inversé a (r) = c, vous prouvez que q = \ frac {a – c} {x – r} est un polynôme.
Si vous comprenez les détails du protocole ou des mécanismes internes à l’avance, vous pouvez trouver des moyens de contourner ou de casser ces protocoles.Des opérations ou des méthodes spécifiques peuvent être mentionnées ensuite pour y parvenir.Par exemple, pour satisfaire l’équation A (\ \ Omega * r), vous pouvez définir un (R) sur 0, puis faire une ligne droite passant à travers ces deux points.
Pour éviter ces attaques, nous devons sélectionner R après que l’attaquant a fourni un (Fiat-Shamir est une technologie utilisée pour améliorer la sécurité du protocole, en évitant les attaques en définissant certains paramètres sur une certaine valeur de hachage. Les paramètres doivent provenir d’un ensemble suffisamment grand Pour s’assurer que l’attaquant ne peut pas prédire ou deviner ces paramètres, améliorant ainsi la sécurité du système.
Dans le protocole et Starks basés sur la courbe elliptique au cours de la période 2019, ce problème est simple: tous nos mathématiques sont effectuées sur des nombres de 256 bits, afin que nous puissions sélectionner R comme numéro aléatoire 256 bits afin que nous puissions le faire maintenant.Cependant, dans Starks sur des champs plus petits, nous avons un problème: il n’y a que environ 2 milliards de valeurs R possibles à choisir, donc un attaquant qui veut forger des preuves n’a besoin que de 2 milliards de fois, bien que la charge de travail soit élevée, Mais pour un attaquant déterminé, cela peut encore être fait!
Il y a deux solutions à ce problème:
-
Effectuer plusieurs vérifications aléatoires
-
Champs prolongés
Le moyen le plus simple et le plus efficace d’effectuer plusieurs vérifications aléatoires: au lieu de vérifier une coordonnée, il est préférable de vérifier quatre coordonnées aléatoires à plusieurs reprises.Ceci est théoriquement possible, mais il y a des problèmes d’efficacité.Si vous avez affaire à un polynôme avec un degré inférieur à une certaine valeur et opérant sur un domaine d’une certaine taille, un attaquant peut réellement construire un polynôme malveillant qui semble normal dans ces positions.Par conséquent, s’ils peuvent briser avec succès le protocole est une question probabiliste, donc le nombre de cycles de vérification doit être augmenté pour améliorer la sécurité globale et assurer une défense efficace contre les attaquants.
Cela conduit à une autre solution: le domaine étendu, le domaine étendu est similaire au pluriel, mais il est basé sur des domaines finis.Nous introduisons une nouvelle valeur, désignée comme α \ alphaα, et déclarons qu’elle satisfait une certaine relation, comme α2 = une certaine valeur \ alpha ^ 2 = \ text {une certaine valeur} α2 = une certaine valeur.De cette façon, nous créons une nouvelle structure mathématique qui permet des opérations plus complexes sur des domaines finis.Dans ce domaine étendu, le calcul de la multiplication devient une multiplication en utilisant la nouvelle valeur α \ alphaα.Nous pouvons désormais manipuler des paires de valeurs dans des domaines étendus, pas seulement des nombres uniques.Par exemple, si nous travaillons sur des champs comme Mersenne ou Babybear, une telle extension nous permet d’avoir plus de choix de valeur, améliorant ainsi la sécurité.Pour augmenter davantage la taille du champ, nous pouvons appliquer à plusieurs reprises la même technique.Puisque nous avons utilisé α \ alphaα, nous devons définir une nouvelle valeur qui, dans Mersenne31, se manifeste comme sélectionnant α \ alphaα tel que α2 = une certaine valeur \ alpha ^ 2 = \ text {une certaine valeur} α2 = une certaine valeur.

Code (vous pouvez l’améliorer avec Karatsuba)
En étendant le domaine, nous avons maintenant suffisamment de valeurs pour choisir pour répondre à nos besoins de sécurité.Si vous avez affaire à un polynôme avec un degré plus petit que le DDD, chaque tour peut assurer une sécurité 104 bits.Cela signifie que nous avons une sécurité suffisante.Si vous devez atteindre un niveau de sécurité plus élevé, tel que 128 bits, nous pouvons ajouter des travaux informatiques supplémentaires au protocole pour améliorer la sécurité.
Les domaines étendus ne sont utilisés que dans le protocole FRI (Fast Reed-Solomon Interactive) et d’autres scénarios qui nécessitent des combinaisons linéaires aléatoires.La plupart des opérations mathématiques sont toujours effectuées sur des champs de base, qui sont généralement des champs qui sont modulo PPP ou QQQ.Pendant ce temps, presque toutes les données hachées se font sur le champ de base, donc chaque valeur n’a que quatre octets hachés.Cela peut profiter de l’efficacité des petits champs, tout en utilisant des champs plus grands lorsque des améliorations de sécurité sont nécessaires.
Fri régulier
Lors de la construction de snark ou de Stark, la première étape est généralement une arithmétisation.Il s’agit de traduire des problèmes de calcul arbitraires en une équation où certaines variables et coefficients sont des polynômes.Plus précisément, cette équation ressemble généralement à p (x, y, z) = 0p (x, y, z) = 0, où p est un polynôme, x, y et z est le paramètre donné, et le solveur doit Fournissez les valeurs de X et Y.Une fois qu’une telle équation est présente, la solution de l’équation correspond à la solution du problème de calcul sous-jacent.
Pour prouver que vous avez une solution, vous devez prouver que la valeur que vous proposez est en effet un polynôme raisonnable (plutôt qu’une fraction, ou à certains endroits, il ressemble à un polynôme et dans d’autres endroits, il s’agit d’un polynôme différent, etc.) , Et ces polynômes ont un certain degré maximum.Pour ce faire, nous utilisons une technique de combinaison linéaire aléatoire étape par étape:
-
Supposons que vous ayez une valeur d’évaluation du polynôme A et que vous voulez prouver que son diplôme est inférieur à 2 ^ {20}
-
Considérons le polynôme b (x ^ 2) = a (x) + a (-x), c (x ^ 2) = \ frac {a (x) – a (-x)} {x}
-
D est une combinaison linéaire aléatoire de B et C, c’est-à-dire d = b + rcd = b + rcd = b + rc, où r est un coefficient aléatoire.
Essentiellement, ce qui se passe B est les isolats B même les coefficients A, et isolate les coefficients étranges.Étant donné B et C, vous pouvez restaurer le polynôme d’origine a: a (x) = b (x ^ 2) + xc (x ^ 2).Si le degré de A est en effet inférieur à 2 ^ {20}, alors les degrés de B et C seront les degrés de A et les degrés de A, respectivement, moins 1.Parce que la combinaison de termes égaux et étranges n’augmente pas le degré.Étant donné que D est une combinaison linéaire aléatoire de B et C, le degré de D devrait également être le degré de A, ce qui vous permet de vérifier si le degré de A répond aux exigences par le degré de D.
Premièrement, le FRI simplifie le processus de vérification en simplifiant le problème de prouver le degré polynomial de D au problème de prouver le degré polynomial de D / 2.Ce processus peut être répété plusieurs fois, simplifiant le problème à mi-chemin à chaque fois.
Le principe de travail du ven est de répéter ce processus simplifié.Par exemple, si vous commencez par la preuve que le polynôme est D, à travers une série d’étapes, vous finirez par prouver que le polynôme est D / 2.Après chaque simplification, le degré du polynôme généré est progressivement réduit.Si la sortie d’une étape n’est pas le degré polynomial attendu, ce cycle de chèques échouera.Si quelqu’un essaie de pousser un polynôme qui n’est pas un degré D à travers cette technique, alors dans le deuxième cycle de sortie, le diplôme aura une certaine probabilité qu’il ne répondra pas aux attentes, et au troisième tour, il y aura plus de chances Pour être une situation de non-conformité.Cette conception peut détecter et rejeter efficacement les entrées qui ne répondent pas aux exigences.Si l’ensemble de données est égal à un polynôme avec un degré D à la plupart des endroits, cet ensemble de données a le potentiel d’être validé par le ven.Cependant, afin de construire un tel ensemble de données, un attaquant doit connaître le polynôme réel, donc même une légère preuve imparfaite indique que le prover est capable de générer une « vraie » preuve.
Examinons de plus près ce qui se passe ici et les propriétés nécessaires pour que cela fonctionne.À chaque étape, nous réduisons la moitié du nombre de polynômes, tout en réduisant également la moitié de l’ensemble des points (l’ensemble des points sur lesquels nous nous concentrons).Le premier est la clé pour que le protocole FRI (Fast Reed-Solomon Interactive) fonctionne correctement.Ce dernier fait fonctionner l’algorithme extrêmement rapide: comme l’échelle de chaque tour est réduite de moitié par rapport au tour précédent, le coût de calcul total est O (n), pas O (n * log (n)).
Pour obtenir une réduction progressive du domaine, une cartographie de deux à un est utilisée, c’est-à-dire que chaque point est mappé à l’un des deux points.Cette cartographie nous permet de réduire la taille de notre ensemble de données en deux.Un avantage important de cette cartographie deux à un est qu’elle est reproductible.Autrement dit, lorsque nous appliquons ce mappage, l’ensemble de résultats résultant conserve toujours les mêmes propriétés.Supposons que nous commencions avec un sous-groupe multiplicatif.Ce sous-groupe est un ensemble où chaque élément x a également son multiple 2x dans l’ensemble.Si vous effectuez une opération carrée sur l’ensemble S (c’est-à-dire la carte de chaque élément x dans l’ensemble sur x ^ 2), le nouvel ensemble S ^ 2 conserve les mêmes attributs.Cette opération nous permet de continuer à réduire la taille de l’ensemble de données jusqu’à ce que nous nous retrouvions avec une seule valeur à gauche.Bien qu’en théorie, nous pouvons réduire l’ensemble de données à une seule valeur à gauche, en pratique, il s’arrête généralement avant qu’un ensemble plus petit ne soit atteint.
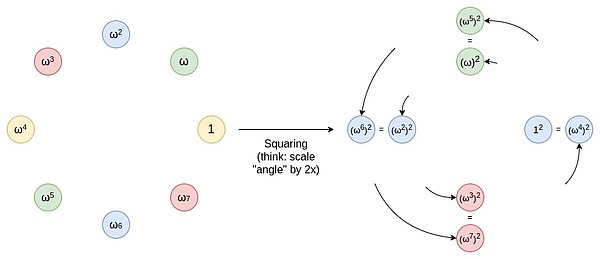
Vous pouvez considérer cette opération comme un processus d’extension d’une ligne (par exemple, un segment ou un arc) sur la circonférence, ce qui lui fait tourner deux tours autour de la circonférence.Par exemple, si un point est à une position de degré x sur la circonférence, alors après cette opération, il passe à une position de 2x degrés.Chaque point sur la circonférence à une position de 0 à 179 degrés a un point correspondant à une position de 180 à 359 degrés, et ces deux points se chevaucheront.Cela signifie que lorsque vous mappez un point de x à 2x degrés, il coïncide avec une position à x + 180 degrés.Ce processus peut être répété.Autrement dit, vous pouvez appliquer cette opération de mappage plusieurs fois, à chaque fois, se déplaçant des points sur la circonférence à leur nouvelle position.
Pour rendre la technique de cartographie efficace, la taille du sous-groupe de multiplication d’origine doit avoir une grande puissance de 2 comme facteur.BabyBear est un système avec un module spécifique dont le module est une valeur telle que son sous-groupe de multiplication maximal contient toutes les valeurs non nulles, de sorte que la taille du sous-groupe est de 2k – 1 (où k est le nombre de bits du module).Ce sous-groupe de taille est très adapté à la technique ci-dessus car il permet à la réduction efficacement du degré du polynôme en appliquant à plusieurs reprises des opérations de cartographie.Dans Babybear, vous pouvez sélectionner un sous-groupe de taille 2 ^ k (ou utiliser directement l’ensemble entier), puis appliquer la méthode pro pour réduire progressivement le degré de polynôme à 15, et vérifier le degré du polynôme à la fin.Cette méthode utilise les propriétés du module et la taille des sous-groupes de multiplication, ce qui rend le processus de calcul très efficace.Mersenne31 est un autre système avec un module d’une certaine valeur, de sorte que la taille du sous-groupe de multiplication est de 2 ^ 31 – 1.Dans ce cas, le sous-groupe de multiplication n’a qu’une seule puissance de 2 comme facteur, ce qui ne le fait diviser qu’une seule fois.Le traitement ultérieur ne s’applique plus aux techniques ci-dessus, c’est-à-dire qu’il est impossible d’utiliser FFT pour effectuer une réduction efficace de degré polynomial comme Babybear.
Le domaine Mersenne31 est idéal pour les opérations arithmétiques dans les opérations CPU / GPU 32 bits existantes.En raison de ses caractéristiques du module (par exemple, 2 ^ {31} – 1), de nombreuses opérations peuvent être effectuées en utilisant des opérations de bits efficaces: si le résultat de deux nombres dépasse le module, vous pouvez déplacer le résultat du module. réduire à la plage appropriée.L’opération de déplacement est une opération très efficace.Dans les opérations de multiplication, des instructions spécifiques du processeur (généralement appelées instructions de déplacement élevé) peuvent être utilisées pour traiter les résultats.Ces instructions peuvent calculer efficacement la partie élevée de la multiplication, améliorant ainsi l’efficacité de l’opération.Dans le domaine Mersenne31, en raison des caractéristiques ci-dessus, les opérations arithmétiques sont environ 1,3 fois plus rapides que dans le domaine Babybear.Mersenne31 fournit une efficacité informatique plus élevée.Si le FRI peut être mis en œuvre dans le domaine Mersenne31, cela améliorera considérablement l’efficacité informatique et rendra les applications FRI plus efficaces.
Cercle ven
C’est l’intelligence des étoiles du cercle.Ce groupe est composé de tous les points qui remplissent certaines conditions spécifiques, par exemple, x ^ 2 mod p est égal à un ensemble de points où une valeur spécifique.
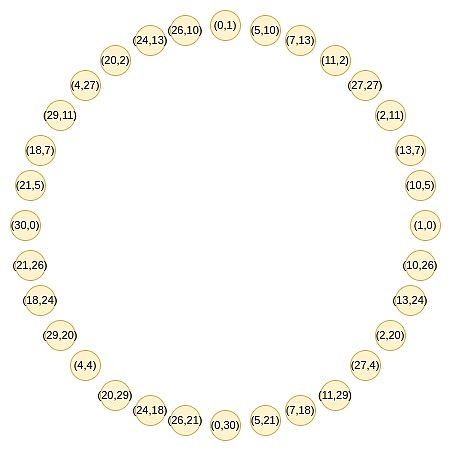
Ces points suivent une règle d’addition, que vous pourriez être familière si vous avez fait la trigonométrie ou la multiplication complexe récemment.
(x_1, y_1) + (x_2, y_2) = (x_1x_2 – y_1y_2, x_1y_2 + x_2y_1)
La double forme est:
2 * (x, y) = (2x ^ 2 – 1, 2xy)
Maintenant, concentrons-nous sur les points sur la position impair sur ce cercle:
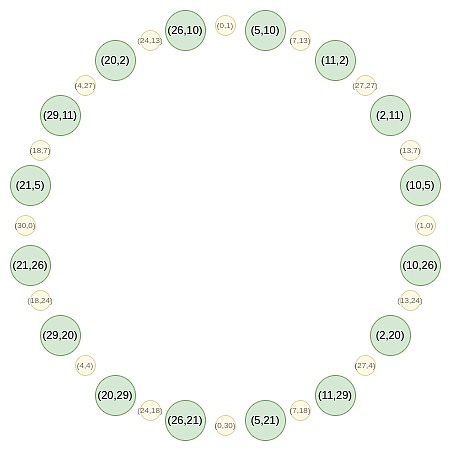
Tout d’abord, nous convergeons tous les points sur une ligne droite.Les formes équivalentes des formules B (x²) et C (x²) que nous utilisons en VNA régulière sont:
f_0 (x) = \ frac {f (x, y) + f (x, -y)} {2}
Ensuite, nous pouvons faire des combinaisons linéaires aléatoires pour obtenir un P (x) unidimensionnel, qui est défini sur un sous-ensemble de la ligne X:
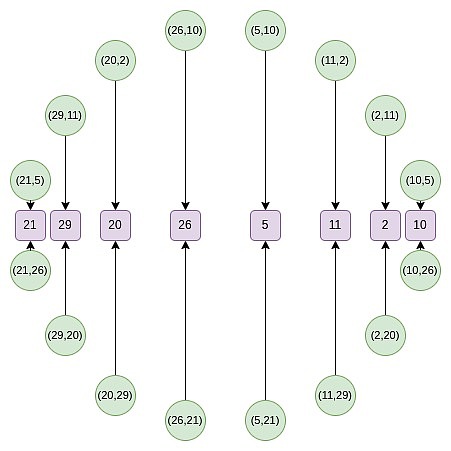
À partir du deuxième tour, la cartographie a changé:
f_0 (2x ^ 2-1) = \ frac {f (x) + f (-x)} {2}
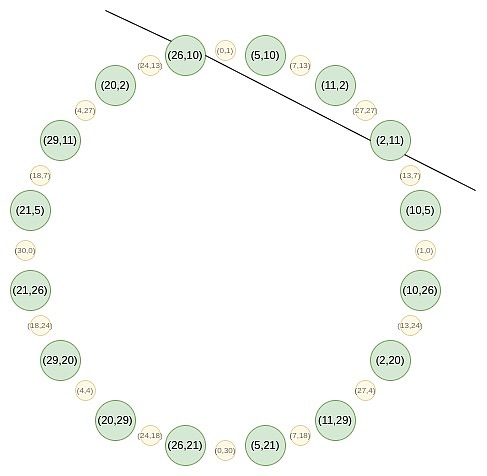
Cette cartographie réduit en fait la taille de l’ensemble ci-dessus de moitié à chaque fois, et ce qui se passe ici, c’est que chaque X représente deux points dans un sens: (x, y) et (x, -y).Et (x → 2x ^ 2 – 1) est la règle de multiplication ponctuelle ci-dessus.Par conséquent, nous convertissons les coordonnées X de deux points opposés sur le cercle en coordonnées x des points multipliés.
Par exemple, si nous prenons la deuxième valeur du nombre à droite du cercle sur le deuxième nombre et appliquons le mappage 2 → 2 (2 ^ 2) – 1 = 7, nous obtenons le résultat de 7.Si nous revenons au cercle d’origine, (2, 11) est le troisième point de la droite, donc après l’avoir multiplié, nous obtenons le sixième point de la droite, c’est-à-dire (7, 13).
Cela aurait pu être fait dans un espace bidimensionnel, mais fonctionner dans un espace unidimensionnel rendrait le processus plus efficace.
Coucle FFTS
Un algorithme étroitement lié au FRI est FFT, qui convertit les valeurs d’évaluation d’un polynôme avec un degré inférieur à n à n coefficients du polynôme.Le processus de FFT est similaire à FRI, sauf qu’au lieu de générer des combinaisons linéaires aléatoires de F_0 et F_1 à chaque étape, FFT réalise récursivement les FFT de dimension sur eux et prend la sortie de FFT (F_0) en tant que coefficient uniforme, prend le Sortie de FFT (F_1) comme coefficient impair.
Circle Group prend également en charge FFT, qui est construit de la même manière que le ven.Cependant, une différence clé est que les objets traités par Circle FFT (et Circle Fri) ne sont pas strictement polynomiaux.Au lieu de cela, ils sont ce qu’on appelle mathématiquement l’espace Riemann-Roch: dans ce cas, le polynôme est encerclé modulairement (x ^ 2 + y ^ 2 – 1 = 0).C’est-à-dire que nous traitons tout multiple de x ^ 2 + y ^ 2 – 1 comme zéro.Une autre façon de le comprendre est: nous n’autorisons qu’une seule puissance de y: une fois que le terme y ^ 2 apparaît, nous le remplaçons par 1 – x ^ 2.
Cela signifie également que les coefficients sorties par le cercle FFT ne sont pas monomiaux en tant que FRI ordinaire (par exemple, si la sortie FRI régulière est [6, 2, 8, 3], alors nous savons que cela signifie p (x) = 3x ^ 3 + 8x ^ 2 + 2x + 6).Au lieu de cela, les coefficients de Circle FFT sont la base de Circle FFT: {1, y, x, xy, 2x ^ 2 – 1, 2x ^ 2y – y, 2x ^ 3 – x, 2x ^ 3y – xy, 8x ^ 4 – 8x ^ 2 + 1 …}
La bonne nouvelle est qu’en tant que développeur, vous pouvez presque complètement ignorer cela.Starks ne vous demandera jamais de connaître les coefficients.Au lieu de cela, vous stockez simplement le polynôme comme un ensemble de valeurs d’évaluation sur un domaine spécifique.Le seul endroit pour utiliser FFT est d’effectuer (similaire à l’espace Riemann-Roch) à faible degré: compte tenu des valeurs n, générez des valeurs k * n, toutes sur le même polynôme.Dans ce cas, vous pouvez utiliser FFT pour générer des coefficients, ajouter (K-1) N Zeros à ces coefficients, puis utiliser la FFT inverse pour obtenir un ensemble plus important de valeurs d’évaluation.
Circle FFT n’est pas le seul type FFT spécial.Les FFT de courbe elliptique sont plus puissantes car elles peuvent travailler sur n’importe quel domaine fini (domaine principal, domaine binaire, etc.).Cependant, ECFFT est plus complexe et inefficace, donc comme nous pouvons utiliser Circle FFT sur p = 2 ^ {31} -1, nous avons choisi de l’utiliser.
De là, nous allons plus profondément dans des détails plus obscurs, et les détails de la mise en œuvre de l’implémentation de Circle Starks sont différents de ceux de Starks ordinaires.
Quotidien
Dans le protocole Stark, une opération commune consiste à effectuer des opérations quotidiennes sur des points spécifiques, qui peuvent être sélectionnés intentionnellement ou au hasard.Par exemple, si vous voulez prouver que p (x) = y, vous pouvez le faire par:
Quotient calculant: étant donné le polynôme p (x) et la constante y, le quotient informatique q = {p – y} / {x – x}, où x est le point sélectionné.
Proof Polynomial: la preuve Q est un polynôme, pas une valeur fractionnaire.De cette façon, il est prouvé que p (x) = y est vrai.
De plus, dans le protocole en profondeur, la sélection aléatoire des points d’évaluation consiste à réduire le nombre de branches de Merkle, améliorant ainsi la sécurité et l’efficacité du protocole FRI.
Lorsque vous traitez avec le protocole Stark du groupe Circle, car aucune fonction linéaire ne peut être transmise à travers un seul point, différentes techniques doivent être utilisées pour remplacer la méthode de fonctionnement du quotient traditionnel.Cela nécessite généralement la conception de nouveaux algorithmes en utilisant les propriétés géométriques uniques au groupe Circle.
Dans le groupe Circle, vous pouvez construire une fonction tangente à tangente en un point (p_x, p_y), mais cette fonction aura un grand nombre de 2 à travers le point, c’est-à-dire pour faire un polynôme le multiple d’une fonction linéaire , qui doit satisfaire une condition plus stricte que d’être nul uniquement à ce moment-là.Par conséquent, vous ne pouvez pas simplement prouver les résultats de l’évaluation à un moment donné.Alors, comment devons-nous y faire face?
Nous avons dû relever ce défi, prouvé en l’évaluant à deux points, ajoutant ainsi un point virtuel sur lequel nous n’avons pas besoin de nous concentrer.

Fonction de ligne: ax + par + c.Si vous le transformez en une équation et le forcez à égaler 0, alors vous pourriez le reconnaître comme une ligne dans ce qu’on appelle une forme standard dans les mathématiques du secondaire.
Si nous avons un polynôme P est égal à y_1 à x_1 et y_2 à x_2, nous pouvons choisir une fonction d’interpolation L, qui équivaut à y_1 à x_1 et y_2 à x_2.Cela peut être simplement exprimé en l = \ frac {y_2 – y_1} {x_2 – x_1} \ cdot (x – x_1) + y_1.
Ensuite, nous prouvons que p est égal à y_1 à x_1 et y_2 à x_2, en soustrayant L (de sorte que p – l est zéro aux deux points), et par l (c’est-à-dire une fonction linéaire entre x_2 – x_1) divisé par l à à Prouvez que le quotient Q est un polynôme.
Disparaître les polynômes
En Stark, l’équation polynomiale que vous essayez de prouver ressemble généralement à c (p (x), p ({suivant} (x))) = z (x) ⋅ h (x), où z (x) est un polynôme égal à zéro dans tout le domaine d’évaluation d’origine.En Stark régulier, cette fonction est x ^ n – 1.Dans un Stark circulaire, la fonction correspondante est:
Z_1 (x, y) = y
Z_2 (x, y) = x
Z_ {n + 1} (x, y) = (2 * z_n (x, y) ^ 2) – 1
Notez que vous pouvez déduire le polynôme disparu de la fonction d’effondrement: dans un Stark régulier, vous réutilisez x → x ^ 2, tandis que dans une piste circulaire, vous réutilisez x → 2x ^ 2 – 1.Cependant, pour le premier tour, vous ferez différents traitements car le premier tour est spécial.
Ordre du binaire inversé
Dans Starks, l’évaluation des polynômes n’est généralement pas disposée en ordre « naturel » (par exemple, P (ω), P (ω2),…, P (ωn – 1), mais est basé sur ce que j’appelle l’ordre inverse inverse de l’ordre inverse :
P (\ omega ^ {\ frac {3n} {8}})
Si nous définissons n = 16 et nous nous concentrons uniquement sur les pouvoirs de Ω que nous évaluons, la liste ressemble à ceci:
{0, 8, 4, 12, 2, 10, 6, 14, 1, 9, 5, 13, 3, 11, 7, 15}
Ce type a une propriété clé que les valeurs regroupées au début de l’évaluation du FRI seront adjacentes au type.Par exemple, la première étape des groupes FRI x et -x.Dans le cas de n = 16, ω ^ 8 = -1, ce qui signifie p (ω ^ i)) et (p (-ω ^ i) = p (ω ^ {i + 8}) \).Comme nous pouvons le voir, ce sont exactement les bonnes paires les unes à côté des autres.La deuxième étape des groupes Fri p (ω ^ i), p (ω ^ {i + 4}), p (ω ^ {i + 8}) et p (ω ^ {i + 12}).C’est exactement ce que nous voyons en quatre groupes, etc.Faire cela rend le ven, encore plus d’espace, car il vous permet de fournir une preuve de merkle pour les valeurs qui sont pliées ensemble (ou, si vous pliez des roues k à la fois, toutes les valeurs 2 ^ k).
Dans Circle Starks, la structure de pli est légèrement différente: dans la première étape, nous coupons (x, y) avec (x, -y); Q, sélectionnez P et Q pour que Q ^ I (P) = -Q ^ I (Q), où Q ^ i est une cartographie répétée x → 2x ^ 2-1 I fois.Si nous considérons ces points de la position sur le cercle, alors à chaque étape, cela ressemble au premier point associé au dernier point, au deuxième point associé à l’avant-dernier point, et ainsi de suite.
Afin d’ajuster l’ordre du bit inverse pour refléter cette structure de pliage, nous devons inverser chaque bit sauf le dernier bit.Nous gardons le dernier bit et l’utilisons pour décider de retourner les autres bits.
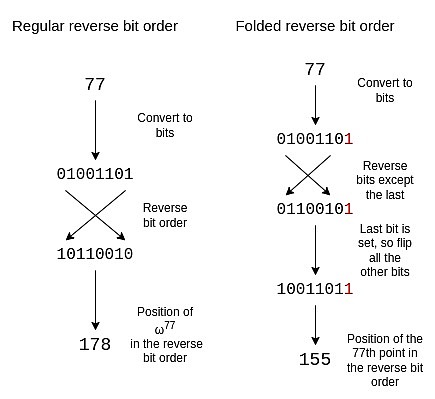
Un ordre bit inverse plié de taille 16 est le suivant:
{0, 15, 8, 7, 4, 11, 12, 3, 2, 13, 10, 5, 6, 9, 14, 1}
Si vous observez le cercle dans la section précédente, vous constaterez que les points 0, 15, 8 et 7 (dans le sens antihoraire de la droite) sont (x, y), (x, -y), (-x, – y) et (-x, y) formes, qui sont exactement ce dont nous avons besoin.
efficacité
Ces protocoles sont très efficaces dans Circle Starks (et généralement des étoiles de premier ordre de 31 bits).Un calcul prouvé en cercle Stark implique généralement plusieurs types de calculs:
1. Arithmétique native: utilisée pour la logique commerciale, comme le comptage.
2. Arithmétique native: utilisée dans la cryptographie, comme les fonctions de hachage comme Poseidon.
3. Trouvez des paramètres: une méthode de calcul générale et efficace qui implémente divers calculs en lisant les valeurs des tables.
La mesure clé de l’efficacité est: lors du suivi informatique, profitez-vous de tout l’espace pour un travail utile ou laissez beaucoup d’espace libre.Dans Snarks dans de grands champs, il y a souvent beaucoup d’espace libre: la logique commerciale et les tables de recherche impliquent généralement des calculs de petits nombres (ces nombres sont souvent inférieurs à n, n est le nombre total d’étapes de calcul, et donc moins de 2 ^ ^ {25 dans la pratique}), mais vous devez toujours payer le coût de l’utilisation d’un champ de taille de taille 2 ^ {256}.Ici, la taille du champ est de 2 ^ {31}, donc l’espace gaspillé n’est pas beaucoup.Les hachats de complexité arithmétiques faibles conçus pour les grondements (comme le poseidon) font pleinement usage de chaque nombre de chaque numéro dans le suivi dans n’importe quel champ.
Binius est une meilleure solution que les Starks de cercle car il vous permet de mélanger les champs de différentes tailles pour un emballage de bits plus efficace.Binius fournit également la possibilité d’effectuer un ajout 32 bits sans augmenter les frais généraux de table de recherche.Cependant, le prix de ces avantages (à mon avis) est qu’ils rendront le concept plus complexe, tandis que Circle Starks (et les Starks réguliers basés sur Babybear) sont relativement simples conceptuellement.
Conclusion: Mon opinion sur Circle Starks
Circle Starks Rien de plus compliqué pour les développeurs que Starks.Au cours du processus de mise en œuvre, les trois questions mentionnées ci-dessus sont essentiellement la différence par rapport au VNE conventionnel.Bien que les mathématiques derrière les polynômes exploités par Circle Fri soient très complexes et qu’il faut un certain temps pour le comprendre et l’apprécier, cette complexité est en fait cachée moins visiblement et que les développeurs ne le ressentent pas directement.
Comprendre le cercle FRI et le cercle FFTS peuvent également être un moyen de comprendre d’autres FFT spéciaux: les plus notables sont les FFT de domaine binaire, telles que les FFT utilisées par Binius et la LibStark précédente, et quelques constructions plus complexes, telles que les FFT courbes elliptiques, ces éléments Les FFT utilisant une cartographie moins à plusieurs peuvent être bien combinées avec l’opération de point de courbe elliptique.
En combinant les technologies Mersenne31, Babybear et Binary Domain comme Binius, nous avons l’impression que nous approchons des limites d’efficacité de la couche de base des étoiles.À ce stade, je m’attends à ce que la direction d’optimisation de Stark aura les points clés suivants:
Arithmétique pour maximiser l’efficacité des fonctions de hachage et des signatures: optimiser les primitives cryptographiques de base telles que les fonctions de hachage et les signatures numériques dans la forme la plus efficace, afin qu’ils puissent obtenir des performances optimales lorsqu’elles sont utilisées dans des preuves frappantes.Cela signifie des optimisations spéciales pour ces primitives afin de réduire les efforts de calcul et d’augmenter l’efficacité.
Effectuer une construction récursive pour permettre plus de parallélisation: la construction récursive fait référence à l’application récursive du processus de preuve stark à différents niveaux, améliorant ainsi la puissance de traitement parallèle.De cette façon, les ressources informatiques peuvent être utilisées plus efficacement et le processus de preuve peut être accéléré.
Les machines virtuelles arithmétiques pour améliorer l’expérience du développeur: le traitement arithmétique des machines virtuelles le rend plus efficace et simple pour les développeurs pour créer et exécuter des tâches informatiques.Cela comprend l’optimisation des machines virtuelles pour une facilité d’utilisation dans des preuves frappantes, l’amélioration de l’expérience des développeurs lors de la création et du test des contrats intelligents ou d’autres tâches informatiques.







