Vitaliks neue Arbeitxploration Circlestarks

Original-Titel: „Exploring Circle Starks“ von Vitalik Buterin, Mitbegründer von Ethereum, zusammengestellt von Chris, Techub News

Die Prämisse, diesen Artikel zu verstehen, besteht darin, dass Sie die Grundprinzipien von Snarks und Starks bereits verstanden haben.Wenn Sie damit nicht vertraut sind, wird empfohlen, die ersten Teile dieses Artikels zu lesen, um die Grundlagen zu erlernen.

In den letzten Jahren besteht der Trend zum Starks -Protokolldesign darin, kleinere Felder zu verwenden.Die frühesten Implementierungen für die Produktion von Starks verwendeten 256-Bit-Felder, die modulare Operationen bei großen Zahlen (wie 21888 … 95617) waren, wodurch diese Protokolle mit elliptischen Kurven-basierten Signaturen kompatibel machten.Dieses Design ist jedoch relativ ineffizient. Es ist nur ein 9. der Berechnungszeit erforderlich.Um dieses Problem zu lösen, wandten sich Starks an kleinere Felder: zuerst Goldillocks, dann Mersenne31 und Babybear.

Diese Verschiebung verbessert die Beweisgeschwindigkeit, wie die Fähigkeit von Starkware, 620.000 Poseidon2 -Hashes pro Sekunde auf einem M3 -Laptop zu beweisen.Dies bedeutet, dass wir, solange wir bereit sind, Poseidon2 als Hash-Funktion zu vertrauen, das Problem bei der Entwicklung eines effizienten ZK-EVM lösen können.Wie funktionieren diese Technologien?Wie werden diese Beweise auf kleineren Feldern festgelegt?Wie vergleichen sich diese Protokolle mit Lösungen wie Binius?In diesem Artikel werden diese Details untersucht und sich speziell auf ein Schema namens Circle Starks (STWO in Starkware, Plonky3 in Polygon und meine eigene Version in Python) konzentrieren, die einzigartige Eigenschaften aufweist, die mit dem Feld Mersennee31 kompatibel sind.

Häufige Probleme bei der Verwendung kleinerer mathematischer Felder

Bei der Erstellung von Hash-basierten Beweisen (oder einer beliebigen Art von Beweis) besteht eine sehr wichtige Technik darin, die Eigenschaften von Polynomen indirekt zu überprüfen, indem die Ergebnisse der Bewertung von Polynomen an zufälligen Punkten geprüft werden.Dieser Ansatz kann den Beweisprozess erheblich vereinfachen, da die Bewertung an zufälligen Punkten normalerweise viel einfacher ist als mit dem gesamten Polynom.

Angenommen, von einem Proof -System muss Sie einen Commit für Polynome generieren, a, muss a^3 (x) + x – a (\ Omega*x) = x^n (eine sehr verbreitete im ZK -Snark Protokoll -Proof -Typ).Das Protokoll kann Sie bitten, eine zufällige Koordinate auszuwählen?Dann beweisen Sie, dass q = \ frac {a – c} {x – r} ein Polynom ist.

Wenn Sie die Details des Protokolls oder der internen Mechanismen im Voraus verstehen, finden Sie möglicherweise Möglichkeiten, diese Protokolle zu umgehen oder zu knacken.Anschließend können spezifische Operationen oder Methoden erwähnt werden, um dies zu erreichen.Um beispielsweise die A (\ Omega * r) -Abgleis zu erfüllen, können Sie A (r) auf 0 einstellen und dann eine gerade Linie durch diese beiden Punkte durchführen.

Um diese Angriffe zu verhindern, müssen wir R auswählen, nachdem der Angreifer A bereitgestellt hat (Fiat-Shamir ist eine Technologie, die zur Verbesserung der Protokollsicherheit verwendet wird, wodurch Angriffe vermieden werden, indem bestimmte Parameter auf einen bestimmten Hash-Wert festgelegt werden. Um sicherzustellen, dass der Angreifer diese Parameter nicht vorhersagen oder erraten kann, um die Sicherheit des Systems zu verbessern.

In dem elliptischen Kurvenprotokoll und Starks im Zeitraum 2019 ist dieses Problem einfach: Alle unsere Mathematik werden mit 256-Bit-Zahlen durchgeführt, sodass wir R als zufällige 256-Bit-Nummer auswählen können, damit wir es jetzt tun können.In Starks auf kleineren Feldern haben wir jedoch ein Problem: Es stehen nur etwa 2 Milliarden mögliche R -Werte zur Auswahl, so Aber für einen Angreifer, der entschlossen ist, kann es immer noch getan werden!

Es gibt zwei Lösungen für dieses Problem:

• Führen Sie mehrere zufällige Überprüfungen durch

• Erweiterte Felder

Der einfachste und effektivste Weg, um mehrere zufällige Überprüfungen durchzuführen: Anstatt auf eine Koordinate zu überprüfen, ist es besser, wiederholt vier zufällige Koordinaten zu überprüfen.Dies ist theoretisch machbar, aber es gibt Effizienzprobleme.Wenn Sie mit einem Polynom mit einem Grad kleiner als einem bestimmten Wert zu tun haben und auf einer Domäne einer bestimmten Größe arbeiten, kann ein Angreifer tatsächlich ein böswilliges Polynom erstellen, das in diesen Positionen normal aussieht.Es ist daher eine probabilistische Frage, ob sie das Protokoll erfolgreich brechen können, daher muss die Anzahl der Schecksrunden erhöht werden, um die Gesamtsicherheit zu verbessern und eine wirksame Verteidigung gegen Angreifer zu gewährleisten.

Dies führt zu einer anderen Lösung: Erweiterte Domäne, erweiterte Domäne ähnelt dem Plural, basiert jedoch auf endlichen Domänen.Wir führen einen neuen Wert ein, der als α \ alphaα bezeichnet wird, und erklären, dass er eine bestimmte Beziehung erfüllt, wie z.Auf diese Weise erstellen wir eine neue mathematische Struktur, die komplexere Operationen auf endlichen Domänen ermöglicht.In dieser erweiterten Domäne wird die Berechnung der Multiplikation zu einer Multiplikation mit dem neuen Wert α \ alphaα.Wir können jetzt Wertpaare in erweiterten Domänen manipulieren, nicht nur in einzelnen Zahlen.Wenn wir beispielsweise an Feldern wie Mersenne oder Babybear arbeiten, ermöglicht eine solche Erweiterung mehr Wertschöpfung, wodurch die Sicherheit verbessert wird.Um die Größe des Feldes weiter zu erhöhen, können wir wiederholt dieselbe Technik anwenden.Da wir α \ alphaα verwendet haben, müssen wir einen neuen Wert definieren, der sich in Mersenne31 als Auswahl von α \ alphaα so manifestiert, dass α2 = ein gewisser Wert \ alpha^2 = \ text {ein gewisses Wert} α2 = einiger Wert.

Code (Sie können es mit Karatsuba verbessern)

Durch die Erweiterung der Domäne haben wir jetzt genügend Werte, um unsere Sicherheitsanforderungen zu erfüllen.Wenn Sie mit einem Polynom mit einem Grad kleiner als DDD zu tun haben, kann jede Runde 104-Bit-Sicherheit bieten.Dies bedeutet, dass wir über ausreichende Sicherheit verfügen.Wenn Sie ein höheres Sicherheitsniveau erreichen müssen, z. B. 128 Bit, können wir dem Protokoll zusätzliche Computerarbeiten hinzufügen, um die Sicherheit zu verbessern.

Erweiterte Domänen werden nur in FRI-Protokoll (Fast Reed-Solomon Interactive) und anderen Szenarien verwendet, die zufällige lineare Kombinationen erfordern.Die meisten mathematischen Operationen werden weiterhin auf grundlegenden Feldern durchgeführt, bei denen es sich normalerweise um Felder handelt, die Modulo PPP oder QQQ sind.In der Zwischenzeit werden fast alle Hashed -Daten auf dem Basisfeld erfolgen, sodass jeder Wert nur vier Bytes -Hashed hat.Dies kann die Effizienz kleiner Felder nutzen, während größere Felder verwendet werden, wenn Sicherheitsverbesserungen erforderlich sind.

Regulärer Fr

Beim Bauen von Snark oder Stark ist der erste Schritt normalerweise die Arithmetisierung.Dies soll willkürliche Rechenprobleme in eine Gleichung umsetzen, in der einige Variablen und Koeffizienten Polynome sind.Insbesondere sieht diese Gleichung normalerweise wie P (x, y, z) = 0p (x, y, z) = 0 aus, wobei p ein Polynom ist, x, y und z der angegebene Parameter, und der Löser muss zu Geben Sie die Werte von x und y an.Sobald eine solche Gleichung vorhanden ist, entspricht die Lösung der Gleichung der Lösung des zugrunde liegenden Rechenproblems.

Um zu beweisen, dass Sie eine Lösung haben, müssen Sie beweisen, dass der von Ihnen vorgeschlagene Wert tatsächlich ein vernünftiges Polynom ist (und nicht an einigen Stellen aussieht es wie ein Polynom und an anderen Stellen ein anderes Polynom usw.) Und diese Polynome haben einen bestimmten maximalen Grad.Dazu verwenden wir eine schrittweise zufällige lineare Kombinationstechnik:

• Angenommen, Sie haben einen Bewertungswert von Polynom A und möchten beweisen, dass sein Abschluss weniger als 2^{20} beträgt

• Betrachten Sie Polynom b (x^2) = a (x) + a (-x), c (x^2) = \ frac {a (x)-a (-x)} {x}

• D ist eine zufällige lineare Kombination von B und C, d. H. D = B+RCD = B+RCD = B+RC, wobei R ein zufälliger Koeffizient ist.

Im Wesentlichen ist B -Isolate sogar Koeffizienten a und isoliert ungerade Koeffizienten.Mit B und C können Sie das ursprüngliche Polynom A: a (x) = b (x^2) + xc (x^2) wiederherstellen.Wenn der Grad von A tatsächlich weniger als 2^{20} beträgt, sind die Grad von B und C die Grade von A bzw. die Grade von A, minus 1.Weil die Kombination von geraden und seltsamen Begriffen den Grad nicht erhöht.Da D eine zufällige lineare Kombination von B und C ist, sollte der Grad von D auch der Grad von A sein, sodass Sie überprüfen können, ob der Grad von A den Anforderungen nach dem Grad von D erfüllt

Erstens vereinfacht FR den Verifizierungsprozess, indem es das Problem der Nachweis des polynomialen Grades von D zu dem Problem der Nachweis des polynomialen Grades von D/2 vereinfacht.Dieser Vorgang kann mehrmals wiederholt werden, sodass das Problem jedes Mal auf halbem Weg vereinfacht.

Das Arbeitsprinzip von FR besteht darin, diesen vereinfachten Prozess zu wiederholen.Wenn Sie beispielsweise mit dem Beweis beginnen, dass das Polynom D durch eine Reihe von Schritten ist, werden Sie schließlich beweisen, dass das Polynom d/2 ist.Nach jeder Vereinfachung wird der Grad des erzeugten Polynoms allmählich reduziert.Wenn die Ausgabe einer Stufe nicht der erwartete Polynomgrad ist, schlägt diese Scheckrunde aus.Wenn jemand versucht, ein Polynom voranzutreiben, das durch diese Technik kein Grad D ist, hat der Abschluss eine gewisse Wahrscheinlichkeit, dass er in der zweiten Ausgangsrunde nicht den Erwartungen entspricht, und in der dritten Runde wird es wahrscheinlicher sein Eine Nicht-Konformitätssituation zu sein.Dieses Design kann Eingaben effektiv erkennen und ablehnen, die den Anforderungen nicht entsprechen.Wenn der Datensatz an den meisten Standorten einem Polynom mit einem Grad D entspricht, kann dieser Datensatz durch Fral validiert werden.Um einen solchen Datensatz zu erstellen, muss ein Angreifer das tatsächliche Polynom kennen, sodass selbst ein leicht fehlerhafter Beweis darauf hinweist, dass der Prover in der Lage ist, einen „echten“ Beweis zu erzeugen.

Schauen wir uns genauer an, was hier vor sich geht und welche Eigenschaften erforderlich sind, um diese Arbeit zu machen.In jedem Schritt reduzieren wir die Anzahl der Polynome um die Hälfte und reduzieren gleichzeitig die Anzahl der Punkte (die Punkte, auf die wir uns konzentrieren) um die Hälfte.Ersteres ist der Schlüssel, um das Protokoll des Fri-Protokolls (Fast Reed-Solomon Interactive) richtig zu machen.Letzteres läuft den Algorithmus extrem schnell: Da die Skala jeder Runde im Vergleich zur vorherigen Runde um die Hälfte reduziert wird, sind die Gesamtberechnungskosten o (n), nicht o (n*log (n)).

Um eine allmähliche Verringerung der Domäne zu erreichen, wird eine Zwei-zu-Eins-Zuordnung verwendet, d. H. Jeder Punkt wird einem der beiden Punkte zugeordnet.Mit dieser Zuordnung können wir die Größe unseres Datensatzes in zwei Hälften reduzieren.Ein wichtiger Vorteil dieser Zwei-zu-Eins-Kartierung ist, dass sie wiederholbar ist.Das heißt, wenn wir diese Zuordnung anwenden, behält das resultierende Ergebnissatz die gleichen Eigenschaften bei.Angenommen, wir beginnen mit einer multiplikativen Untergruppe.Diese Untergruppe ist ein Satz S, wobei jedes Element X seine Mehrfach 2x im Satz hat.Wenn Sie eine quadratische Operation auf Set S (d. H. MAP JEDES Element x in der Set auf x^2) durchführen, behält der neue Satz S^2 die gleichen Attribute bei.Mit diesem Vorgang können wir die Größe des Datensatzes weiter reduzieren, bis wir nur noch einen Wert haben.Obwohl wir theoretisch den Datensatz auf nur einen Wert eingrenzen können, wird es in der Praxis normalerweise aufhören, bevor ein kleinerer Satz erreicht ist.

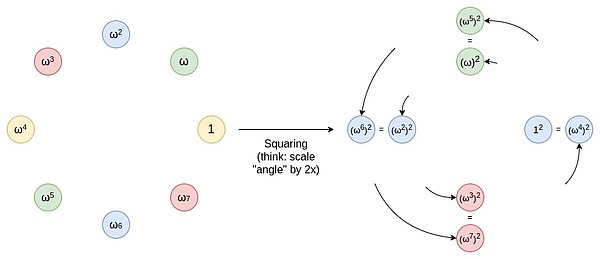
Sie können sich diesen Vorgang als einen Prozess der Erweiterung einer Linie (z. B. eines Segments oder eines Bogens) auf dem Umfang vorstellen, wodurch sich zwei Kurven um den Umfang drehen.Wenn beispielsweise ein Punkt in einer x -Grad -Position auf dem Umfang liegt, bewegt er sich nach dieser Operation in einer Position von 2x Grad.Jeder Punkt auf dem Umfang an einer Position von 0 bis 179 Grad hat einen entsprechenden Punkt an einer Position von 180 bis 359 Grad, und diese beiden Punkte überlappen sich.Dies bedeutet, dass wenn Sie einen Punkt von x bis 2x Grad zuordnen, es mit einer Position bei x+180 Grad zusammenfällt.Dieser Vorgang kann wiederholt werden.Das heißt, Sie können diesen Zuordnungsvorgang mehrmals anwenden, jedes Mal, wenn Sie Punkte auf den Umfang auf ihre neue Position bewegen.

Um die Mapping -Technik effektiv zu machen, muss die Größe der ursprünglichen Multiplikations -Untergruppe eine große Leistung von 2 als Faktor haben.BabyBear ist ein System mit einem bestimmten Modul, dessen Modul ein Wert ist, so dass die maximale Multiplikationsuntergruppe alle Werte ungleich Null enthält, sodass die Größe der Untergruppe 2k – 1 beträgt (wobei k die Anzahl der Bits des Modulus ist).Diese Untergruppe in großer Größe ist für die obige Technik sehr geeignet, da der Grad des Polynoms durch wiederholte Anwendung von Kartierungsvorgängen effektiv reduziert werden kann.In BabyBear können Sie eine Untergruppe der Größe 2^K (oder direkt den gesamten Satz verwenden) auswählen, dann das Fri -Methode anwenden, um den Grad des Polynoms auf 15 allmählich zu reduzieren und den Grad des Polynoms am Ende zu überprüfen.Diese Methode verwendet die Eigenschaften des Moduls und die Größe der Multiplikationsuntergruppen, wodurch der Berechnungsprozess sehr effizient wird.Mersenne31 ist ein weiteres System mit einem Wertmodul, so dass die Größe der Multiplikations -Untergruppe 2^31 – 1 beträgt.In diesem Fall hat die Multiplikations -Untergruppe nur eine Leistung von 2 als Faktor, wodurch sie nur einmal um 2 geteilt wird.Die anschließende Verarbeitung gilt nicht mehr für die oben genannten Techniken, dh es ist unmöglich, FFT zu verwenden, um eine effektive Polynomgrademinderung wie Babybekern durchzuführen.

Die Mersenne31-Domäne ist ideal für arithmetische Operationen in bestehenden 32-Bit-CPU/GPU-Operationen.Aufgrund seiner Moduleigenschaften (z auf den entsprechenden Bereich reduzieren.Der Verschiebungsbetrieb ist ein sehr effizienter Betrieb.Bei Multiplikationsvorgängen können spezifische CPU-Anweisungen (normalerweise als Hochbit-Verschiebungsanweisungen bezeichnet) verwendet werden, um die Ergebnisse zu verarbeiten.Diese Anweisungen können den Hochbit-Teil der Multiplikation effizient berechnen, wodurch die Effizienz des Betriebs verbessert wird.In der Mersenne31 -Domäne sind die arithmetischen Operationen aufgrund der oben genannten Eigenschaften etwa 1,3 -mal schneller als im Babybekarbereich.Mersenne31 bietet eine höhere Recheneffizienz.Wenn Fri in der Mersenne31 -Domäne implementiert werden kann, verbessert dies die Recheneffizienz erheblich und gestaltet Fri -Anwendungen effizienter.

Kreis Fr

Dies ist die Klugheit von Kreisstarks.Diese Gruppe besteht aus allen Punkten, die bestimmte bestimmte Bedingungen erfüllen, z. B. x^2 mod p entspricht einer Reihe von Punkten, bei denen ein bestimmter Wert.

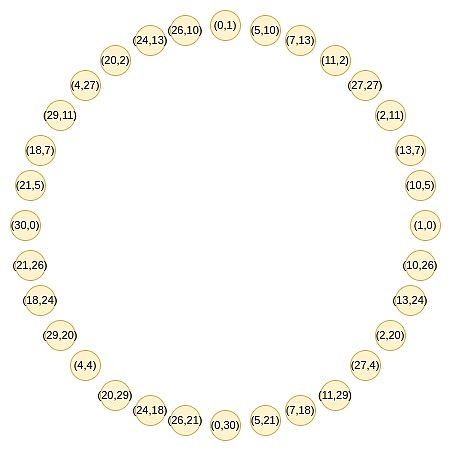
Diese Punkte folgen einer Additionsregel, mit der Sie möglicherweise vertraut sind, wenn Sie in letzter Zeit Trigonometrie oder komplexe Multiplikation durchgeführt haben.

(x_1, y_1) + (x_2, y_2) = (x_1x_2 – y_1y_2, x_1y_2 + x_2y_1)

Die doppelte Form lautet:

2 * (x, y) = (2x^2 – 1, 2xy)

Konzentrieren wir uns nun auf die Punkte auf die seltsame Position in diesem Kreis:

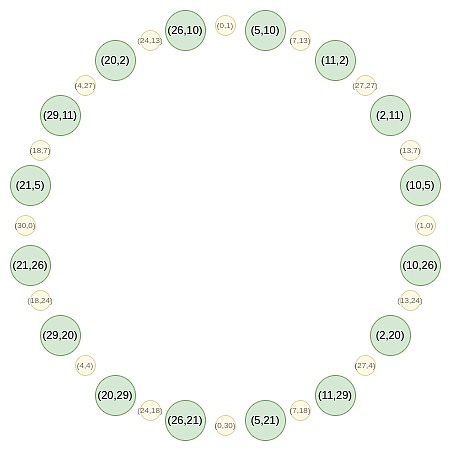
Erstens konvergieren wir alle Punkte auf eine gerade Linie.Die äquivalenten Formen der Formeln B (X²) und C (X²), die wir in regulärer Fr verwenden, sind:

f_0 (x) = \ frac {f (x, y) + f (x, -y)} {2}

Dann können wir zufällige lineare Kombinationen durchführen, um ein eindimensionales P (x) zu erhalten, das auf einer Teilmenge der x-Linie definiert ist:

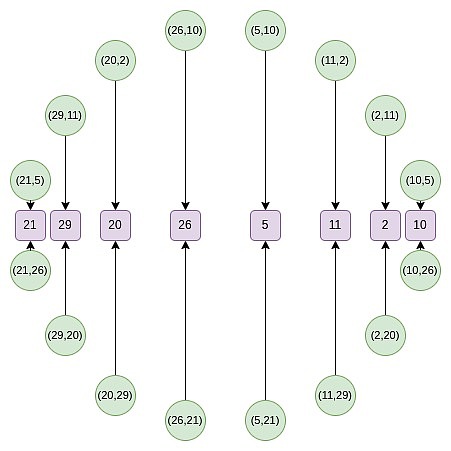
Ab der zweiten Runde änderte sich die Zuordnung:

f_0 (2x^2-1) = \ frac {f (x) + f (-x)} {2}

Diese Zuordnung reduziert tatsächlich die Größe der oben genannten Einstellung jedes Mal um die Hälfte, und hier ist, dass jedes x in gewissem Sinne zwei Punkte darstellt: (x, y) und (x, -y).Und (x → 2x^2 – 1) ist die obige Punktmultiplikationsregel.Daher konvertieren wir die X -Koordinaten von zwei gegenüberliegenden Punkten auf dem Kreis in die X -Koordinaten der multiplizierten Punkte.

Wenn wir beispielsweise den zweiten Wert der Zahl von rechts neben dem Kreis auf der zweiten Zahl nehmen und die Zuordnung 2 → 2 (2^2) – 1 = 7 anwenden, erhalten wir ein Ergebnis von 7.Wenn wir zum ursprünglichen Kreis zurückkehren (2, 11) ist der dritte Punkt von rechts. Nachdem wir ihn multiplizieren, erhalten wir den sechsten Punkt von rechts, d. H. (7, 13).

Dies hätte im zweidimensionalen Raum geschehen können, aber der Betrieb im eindimensionalen Raum würde den Prozess effizienter machen.

Kreis FFTS

Ein Algorithmus, der eng mit Fri verwandt ist, ist FFT, der die N -Bewertungswerte eines Polynoms mit einem Grad von weniger als N zu N -Koeffizienten des Polynoms umwandelt.Der Prozess von FFT ähnelt FR, außer dass FFT in jedem Schritt, anstatt zufällige lineare Kombinationen von F_0 und F_1 zu erzeugen, eine halbgroße FFTs rekursiv durchführt und die Ausgabe von FFT (F_0) als gleichmäßigen Koeffizienten nimmt, die nimmt die nimmt Ausgabe von FFT (F_1) als ungerade Koeffizient.

Die Circle Group unterstützt auch FFT, das ähnlich wie Fr.Ein wesentlicher Unterschied besteht jedoch darin, dass die vom Kreis FFT (und Circle Fr) verarbeiteten Objekte nicht streng polynomisch sind.Stattdessen sind sie mathematisch als Riemann -Roch -Raum bezeichnet: In diesem Fall wird das Polynom modular eingekreist (x^2 + y^2 – 1 = 0).Das heißt, wir behandeln jedes Vielfache von x^2 + y^2 – 1 als Null.Eine andere Möglichkeit, es zu verstehen, ist: Wir erlauben nur eine Kraft von y: Sobald der y^2 -Term erscheint, ersetzen wir ihn durch 1 – x^2.

Dies bedeutet auch, dass die vom Kreis FFT ausgegebenen Koeffizienten nicht wie normale Fr -FRI (zum Beispiel die reguläre Fri -Ausgabe [6, 2, 8, 3] beträgt, dann wissen wir, dass dies P (x) = 3x^ bedeutet 3 + 8x^2 + 2x + 6).Stattdessen sind die Koeffizienten des Kreises FFT die Grundlage für den Kreis FFT: {1, y, x, xy, 2x^2 – 1, 2x^2y – y, 2x^3 – x, 2x^3y – xy, 8x^4 – 8x^2 + 1 …}

Die gute Nachricht ist, dass Sie als Entwickler dies fast vollständig ignorieren können.Starks verlangen nie, dass Sie die Koeffizienten kennen.Stattdessen speichern Sie das Polynom einfach als eine Reihe von Bewertungswerten in einer bestimmten Domäne.Der einzige Ort, an dem FFT verwendet werden kann, besteht darin, (ähnlich dem Riemann-Roch-Raum) eine niedrige Expansion mit niedrigem Grad durchzuführen: gegeben n-Werte, die K*n-Werte erzeugen, alle auf demselben Polynom.In diesem Fall können Sie FFT verwenden, um Koeffizienten zu generieren, (K-1) und Nullen an diese Koeffizienten anzuhängen und dann das inverse FFT zu verwenden, um einen größeren Satz von Bewertungswerten zu erhalten.

Circle FFT ist nicht der einzige spezielle FFT -Typ.Elliptische Kurve -FFTs sind leistungsfähiger, weil sie an jeder endlichen Domäne arbeiten können (Prime Domain, Binärdomäne usw.).ECFFT ist jedoch komplexer und ineffizienter. Da wir also den Kreis FFT auf p = 2^{31} -1 verwenden können, haben wir ihn verwendet, ihn zu verwenden.

Von hier aus werden wir tiefer in einige dunklere Details eingehen, und die Details der Implementierung der Implementierung von Circle Starks unterscheiden sich von denen von regulären Starks.

Quotient

Im Stark -Protokoll besteht ein gängiger Operation darin, Quotientenoperationen an bestimmten Punkten durchzuführen, die absichtlich oder zufällig ausgewählt werden können.Wenn Sie beispielsweise beweisen möchten, dass p (x) = y, können Sie dies tun, wenn Sie:

Rechenquotienten: Angesichts des Polynoms P (x) und des Konstanten y, Computerquotient q = {p – y}/{x – x}, wobei x der ausgewählte Punkt ist.

Proof Polynom: Proof Q ist ein Polynom, kein Bruchwert.Auf diese Weise wird bewiesen, dass p (x) = y wahr ist.

Darüber hinaus besteht die zufällige Auswahl der Bewertungspunkte im Deep-Fr-Protokoll darin, die Anzahl der Merkle-Zweige zu verringern, wodurch die Sicherheit und Effizienz des FRI-Protokolls verbessert werden.

Beim Umgang mit dem Stark -Protokoll der Kreisgruppe müssen verschiedene Techniken verwendet werden, um die herkömmliche Quotientenbetriebsmethode zu ersetzen, da es keine lineare Funktion gibt.Dies erfordert normalerweise das Design neuer Algorithmen unter Verwendung der geometrischen Eigenschaften, die für die Kreisgruppe einzigartig sind.

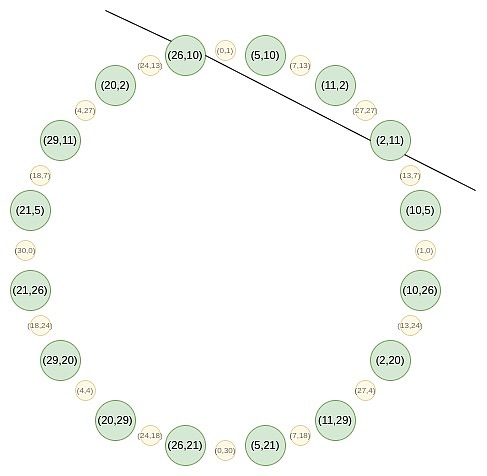
In der Kreisgruppe können Sie eine Tangentenfunktion an einem Punkt (p_x, p_Y) konstruieren, aber diese Funktion hat eine hohe Anzahl von 2 bis zum Punkt, dh ein Polynom zu einer Vielzahl einer linearen Funktion , was einen strengeren Zustand erfüllen muss, als zu diesem Zeitpunkt nur Null zu sein.Daher können Sie die Bewertungsergebnisse an einem Punkt nicht nur beweisen.Wie sollen wir damit umgehen?

Wir mussten diese Herausforderung annehmen, beweist durch die Bewertung an zwei Punkten und fügte so einen virtuellen Punkt hinzu, auf den wir uns nicht konzentrieren müssen.

Zeilenfunktion: AX + durch + c.Wenn Sie es in eine Gleichung verwandeln und es zu gleich 0 erzwingen, erkennen Sie sie möglicherweise als Zeile in einer Standardform in der Mathematik der High School.

Wenn wir ein Polynom -P -Gleichstrom bei x_1 und y_2 bei x_2 haben, können wir eine Interpolationsfunktion L auswählen, die bei x_1 und y_2 bei x_2 gleich y_1 entspricht.Dies kann einfach als l = \ frac {y_2 – y_1} {x_2 – x_1} \ cdot (x – x_1) + y_1 ausgedrückt werden.

Dann beweisen wir, dass p bei x_2 gleich Y_1 und y_2 ist, indem sie L (so dass P – L an beiden Punkten Null ist) und durch L (d. H. Eine lineare Funktion zwischen x_2 – x_1) geteilt durch l bis zu Beweisen Sie, dass der Quotient Q ein Polynom ist.

Verschwundene Polynome

In Stark sieht die Polynomgleichung, die Sie beweisen wollen gleich Null während der ursprünglichen Bewertungsdomäne.In regulärem Stark ist diese Funktion x^n – 1.In einem kreisförmigen Stark ist die entsprechende Funktion:

Z_1 (x, y) = y

Z_2 (x, y) = x

Z_ {n+1} (x, y) = (2 * z_n (x, y)^2) – 1

Beachten Sie, dass Sie das verschwundene Polynom aus der Kollapsfunktion ableiten können: In einem regelmäßigen Stark wiederverwenden Sie x → x^2, während Sie in einem kreisförmigen Stark X → 2x^2 – 1 wiederverwenden.In der ersten Runde werden Sie jedoch unterschiedliche Behandlungen durchführen, da die erste Runde etwas Besonderes ist.

Umgekehrte Bitreihenfolge

In Starks ist die Bewertung von Polynomen normalerweise nicht in der „natürlichen“ Reihenfolge (z. B. P (ω), P (ω2),…, P (ωn – 1) angeordnet, basiert jedoch auf dem, was ich die inverse umgekehrte Bitreihenfolge nenne :

P (\ Omega^{\ frac {3n} {8}})

Wenn wir n = 16 festlegen und sich nur darauf konzentrieren, welche Kräfte von ω bewerten, sieht die Liste so aus:

{0, 8, 4, 12, 2, 10, 6, 14, 1, 9, 5, 13, 3, 11, 7, 15}

Diese Sorte hat eine Schlüsseleigenschaft, die zu Beginn der Fr -Bewertung, die zu Beginn der FRI -Bewertung zusammengefasst sind, in der Sortierung angrenzt.Zum Beispiel der erste Schritt der Fr -Gruppen x und -x.Im Fall von n = 16, ω^8 = -1, was P (ω^i)) und (p (-ω^i) = p (ω^{i+8}) \) bedeutet.Wie wir sehen können, sind dies genau die richtigen Paare nebeneinander.Der zweite Schritt von Fr Gruppern p (ω^i), p (ω^{i+4}), p (ω^{i+8}) und p (ω^{i+12}).Das sind genau das, was wir in vier Gruppen sehen und so weiter.Wenn Sie dies tun, ist Fr noch räumlicher, da Sie einen Merkle-Beweis für Werte bereitstellen, die zusammengeklappt werden (oder, wenn Sie gleichzeitig k-Räder falten, alle 2^k-Werte).

In Kreisstarks ist die Faltungsstruktur etwas unterschiedlich: Im ersten Schritt kombinieren wir (x, y) mit (x, -y); q, wählen Sie P und Q, damit q^i (p) = -q^i (q), wobei Q^i eine Zuordnung ist, die x → 2x^2-1 i mal wiederholt ist.Wenn wir diese Punkte aus der Position im Kreis betrachten, sieht dies in jedem Schritt nach dem ersten Punkt aus, der mit dem letzten Punkt gepaart ist, der zweite Punkt mit dem vorletzten Punkt usw.

Um die umgekehrte Bitreihenfolge anzupassen, um diese Faltstruktur widerzuspiegeln, müssen wir jedes Bit mit Ausnahme des letzten Bits umkehren.Wir behalten das letzte Stück und verwenden es, um zu entscheiden, ob die anderen Teile umdrehen werden sollen.

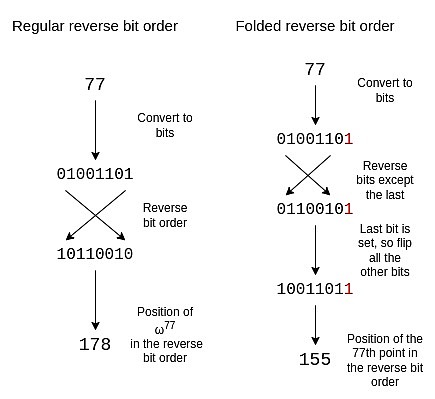
Eine gefaltete inverse Bitreihenfolge von Größe 16 lautet wie folgt:

{0, 15, 8, 7, 4, 11, 12, 3, 2, 13, 10, 5, 6, 9, 14, 1}

Wenn Sie den Kreis im vorherigen Abschnitt beobachten, werden Sie feststellen, dass die Punkte 0, 15, 8 und 7 (gegen den Uhrzeigersinn von rechts) (x, y), (x, -y), (-x, – y) und (-x, y) Formen, die genau das sind, was wir brauchen.

Effizienz

Diese Protokolle sind in Kreisstarks (und im Allgemeinen 31-Bit-Prime-Starks) sehr effizient.Eine im Kreis Stark nachgewiesene Berechnung umfasst normalerweise verschiedene Arten von Berechnungen:

1. Native Arithmetik: Wird für Geschäftslogik wie Zählen verwendet.

2. Native Arithmetik: In Kryptographie verwendet, wie z. B. Hash -Funktionen wie Poseidon.

3. Suchen Sie Parameter: Eine allgemeine und effiziente Berechnungsmethode, die verschiedene Berechnungen durch Lesewerte aus Tabellen implementiert.

Das Hauptmaß für die Effizienz ist: Nutzen Sie bei der Computerverfolgung den gesamten Raum für nützliche Arbeit oder lassen Sie viel freien Speicherplatz.In Snarks in großen Feldern gibt es oft viel freier Speicherplatz: Geschäftslogik- und Nachschlagtabellen beinhalten normalerweise Berechnungen kleiner Zahlen (diese Zahlen sind oft geringer als n, n ist die Gesamtzahl der Berechnungsschritte und daher weniger als 2^ {25 in der Praxis}), aber Sie müssen immer noch die Kosten für die Verwendung eines Bitfeldes der Größe 2^{256} bezahlen.Hier beträgt die Größe des Feldes 2^{31}, so dass der verschwendete Raum nicht viel ist.Hashes mit niedriger arithmetischer Komplexität, die für Snarks (z. B. Poseidon) entwickelt wurden, machen das Beste aus jeder Zahl jeder Zahl in der Verfolgung in jedem Feld.

Binius ist eine bessere Lösung als Circle Starks, da Sie Felder unterschiedlicher Größen für eine effizientere Bitpackung mischen können.Binius bietet auch die Option, 32-Bit-Addition durchzuführen, ohne dass der Überkopf der Nachschlagtabelle erhöht wird.Der Preis dieser Vorteile (meiner Meinung nach) ist jedoch, dass sie das Konzept komplexer machen, während Kreisstarks (und regelmäßige Starks basierend auf Babybear) konzeptionell relativ einfach sind.

Schlussfolgerung: Meine Meinung zu Kreisstarks

Kreisstarks für Entwickler nichts komplizierteres als Starks.Während des Implementierungsprozesses sind die drei oben genannten Fragen im Grunde der Unterschied zu herkömmlichem Fr.Obwohl die Mathematik hinter den von Circle Fr betriebenen Polynomen sehr komplex ist und einige Zeit dauert, um sie zu verstehen und zu schätzen, ist diese Komplexität tatsächlich weniger auffällig versteckt und Entwickler werden sie nicht direkt fühlen.

Das Verständnis von Circle Fr und Circle FFTs kann auch eine Möglichkeit sein, andere spezielle FFTs zu verstehen: Am bemerkenswertesten sind die Binärdomänen -FFTs, wie die von Binius verwendeten FFTs und die vorherigen Libstark, und einige komplexere Konstrukte, wie z. FFTs, die eine weniger zu viele Kartierung verwenden, können mit dem elliptischen Kurvenpunktvorgang gut kombiniert werden.

Durch die Kombination von Mersenne31-, Babybear- und Binärdomänentechnologien wie Binius fühlen wir uns den Effizienzgrenzen der Grundschicht von Starks nähern.Zu diesem Zeitpunkt erwarte ich, dass die Optimierungsrichtung von Stark die folgenden wichtigen Punkte hat:

Arithmetik zur Maximierung der Effizienz von Hash -Funktionen und -signaturen: Optimieren Sie grundlegende kryptografische Primitive wie Hash -Funktionen und digitale Signaturen in die effizienteste Form, damit sie bei Verwendung in Stark -Proofs eine optimale Leistung erzielen können.Dies bedeutet spezielle Optimierungen für diese Primitiven, um den Rechenaufwand zu verringern und die Effizienz zu steigern.

Führen Sie eine rekursive Konstruktion durch, um eine höhere Parallelisierung zu ermöglichen: Rekursive Konstruktion bezieht sich auf die rekursive Anwendung des starken Beweisverfahrens auf verschiedene Ebenen, wodurch die parallele Verarbeitungsleistung verbessert wird.Auf diese Weise können Computerressourcen effizienter und der Beweisverfahren beschleunigt werden.

Arithmetische virtuelle Maschinen zur Verbesserung der Entwicklererfahrung: Die arithmetische Verarbeitung virtueller Maschinen macht es für Entwickler effizienter und einfacher, Computeraufgaben zu erstellen und auszuführen.Dies beinhaltet die Optimierung der virtuellen Maschinen für die Benutzerfreundlichkeit in Stark -Proofs, die Verbesserung der Erfahrung der Entwickler beim Aufbau und Testen von intelligenten Verträgen oder anderen Rechenaufgaben.