Comprendre l’histoire de la preuve de connaissances zéro

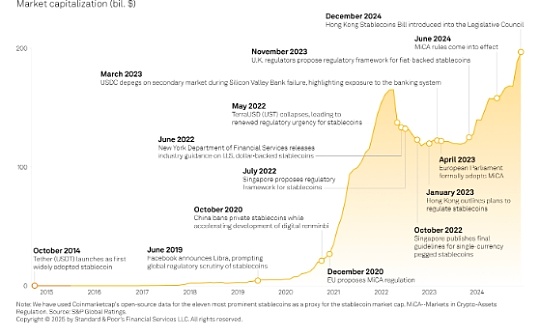
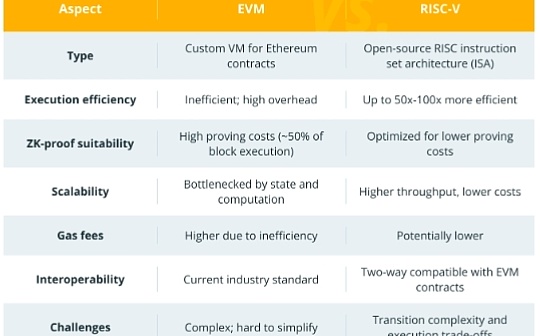
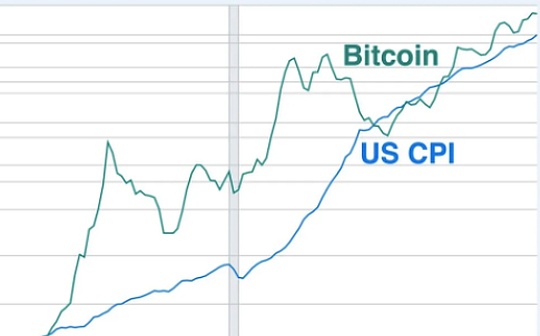
Source: Communauté deglian

La connaissance zéro, la preuve concise et non interactive de la connaissance (ZK-Snarks) sont de puissantes primitives cryptographiques qui permettent à une partie, c’est-à-dire la preuve, de convaincre l’autre partie, qu’une déclaration est vraie sans la révéler. que la validité de cette déclaration.Ils ont attiré une attention généralisée en raison de leurs applications en informatique privée vérifiable, en fournissant une preuve de l’exactitude de l’exécution du programme informatique et en aidant à évoluer les blockchains.Nous pensons que Snarks aura un impact significatif sur la formation de notre monde, comme nous l’avons fait dans notre article^{[6]comme décrit dans.Les SNARKS sont un terme général pour différents types de systèmes de preuve, en utilisant différents schémas d’engagement polynomial (PC), des schémas arithmétiques, des preuves oracle interactives (IOP) ou des preuves vérifiables probabilistes (PCP).Cependant, ces idées et concepts de base remontent au milieu des années 80.Les efforts de développement se sont accélérés considérablement après l’introduction de Bitcoin et Ethereum, ce qui prouve qu’ils sont un cas d’utilisation passionnant et puissant car vous pouvez utiliser des preuves de connaissances zéro (souvent appelées la preuve de validité de ce cas d’utilisation particulier) les élargir.Les SNARKS sont un outil important pour l’évolutivité de la blockchain.Comme Ben-Sasson le décrit, les dernières années ont été témoins de l’épidémie de Cambrien de la crypto[7].Chaque système de preuve présente ses avantages et ses inconvénients, et certains compromis sont pris en compte lors de la conception.Les progrès du matériel, de meilleurs algorithmes, de nouveaux arguments et gadgets ont conduit à des améliorations des performances et à la naissance de nouveaux systèmes.Beaucoup de ces systèmes sont utilisés dans la production et nous continuons à repousser les limites.Aurons-nous un système de preuve universel pour toutes les applications ou plusieurs systèmes pour différents besoins?Nous pensons qu’il y a peu de chances qu’un système de preuve domine toutes les applications parce que:}

1. Diversité des applications.

2. Nous avons différents types de contraintes (sur la mémoire, le temps de vérification, le temps de preuve).

3. Le besoin de robustesse (si un système de preuve est fissuré, nous avons encore d’autres systèmes).

Même si le système de preuve change considérablement, ils ont tous une caractéristique importante: les preuves peuvent être vérifiées rapidement.Les difficultés associées à la modification de la couche sous-jacente (comme Ethereum) sont également résolues en disposant de couches de preuve de preuve de travail et facilement adaptées aux couches qui gèrent de nouveaux systèmes de preuve de travail.

Pour décrire les différentes caractéristiques des SNARKS:

• Hypothèse de mot de passe: fonction de hachage anti-collision, problèmes logarithmiques discrets sur les courbes elliptiques, connaissances exponentielles.

• Paramètres de confiance transparents vs.

• Temps de relecteur: linéaire vs hyperlinéaire.

• Temps du vérificateur: Temps constant, logarithmique, sous-linéaire, linéaire.

• Taille de preuve.

• La commodité de la récursivité.

• Schéma arithmétique.

• Polynomial unaire vs multivarié.

Cet article explorera les origines des SNARKS, certains blocs de construction de base et la montée (et le déclin) de différents systèmes de preuve.Cet article n’a pas l’intention de mener une analyse détaillée du système de preuve.Au lieu de cela, nous nous concentrons sur ceux qui ont un impact sur nous pour le moment.Bien sûr, ces développements ne peuvent être réalisés qu’en fonction de l’excellent travail et des idées des pionniers dans ce domaine.

Connaissances de base

Comme nous l’avons mentionné, la preuve de connaissances zéro n’est pas nouvelle.Des définitions, des fondations, des théorèmes importants et même des protocoles importants ont été établis au milieu des années 80.Certaines des idées et protocoles clés utilisés pour construire des SNARKS modernes ont été proposés dans les années 1990 (protocole Sumcheck), avant même que Bitcoin n’ait émergé (GKR en 2007).Les principaux problèmes adoptés à cette époque étaient principalement liés au manque de cas d’utilisation solides (Internet n’était pas aussi développé que dans les années 1990) et la puissance de calcul requise.

Zéro preuve de connaissances: Origin (1985/1989)

Le domaine de la preuve de connaissances zéro est apparu pour la première fois dans la littérature académique de [Goldwasser, Micali et Rackoff] (https://people.csail.mit.edu/silvio/selected Scientific Papers / Profile Systems / The_kno Wledge_Complexity_Of_Interactive_Poas_Systems.pdf? Ref = blog.lambdaclass .com « Goldwasser, Micali et Rackoff »).Pour une discussion d’origine, vous pouvez vous référer à la vidéo suivante^{[8].Cet article présente les concepts d’exhaustivité, d’exactitude et de connaissances nulles, et fournit la construction de la résidu quadratique et de la non-résiduosité quadratique.}

Sumcheck Accord (1992)

protocole Sumcheck^{[9]Est par Lund, Fortnow, Karloff et Nisan[10]Proposé en 1992.C’est l’un des éléments constitutifs les plus importants pour la preuve d’interaction concise.Il nous aide à réduire la déclaration de somme d’évaluations de plusieurs polynômes à une seule évaluation sur des points sélectionnés au hasard.}

Goldwasser-Kalai-Rothblum (GKR) (2007)

Protocole GKR^{[11]Il s’agit d’un protocole interactif, où le temps d’exécution du prover est linéairement lié au nombre de portes du circuit, tandis que le temps d’exécution du vérificateur est linéairement lié à la taille du circuit.Dans ce protocole, le prover et le vérificateur s’accordent sur un circuit arithmétique de fan-en-deux sur un domaine fini de la profondeur D, où la couche D correspond à la couche d’entrée et la couche 0 correspond à la couche de sortie.Le protocole commence par une déclaration de sortie du circuit et le réduit à une déclaration de la valeur de la couche précédente.Par récursivité, nous pouvons le convertir en une déclaration de l’entrée du circuit, qui peut être facilement vérifiée.Ces réductions sont réalisées grâce au protocole Sumcheck.}

Solution d’engagement polynomial KZG (2010)

KZG Polynomial Engagement Scheme (PCS) Kate, Zaverucha et Goldberg^{[12]Un schéma d’engagement polynomial utilisant des groupes d’appariement bilinéaire a été introduit en 2010.Cet engagement se compose d’un élément de groupe unique et l’engagement peut ouvrir efficacement l’engagement à toute évaluation correcte du polynôme.De plus, en raison de la technologie par lots, plusieurs évaluations peuvent être activées.KZG promet que plusieurs Snarks efficaces tels que Pinocchio, Groth16 et Plonk fournissent les blocs de construction de base.C’est aussi EIP-4844[13]le noyau de.Pour une compréhension intuitive de la technologie de traitement par lots, vous pouvez voir notre pont à peu près Mina-Ethereum[14]Articles.}

Corèges pratiques à l’aide de courbes elliptiques

Les premières constructions pratiques de SNARKS sont apparues en 2013.Ces configurations nécessitent des étapes de prétraitement pour générer des clés de preuve et de vérification et sont spécifiques au programme / circuit.Ces clés peuvent être assez importantes et dépendre de paramètres secrètes inconnus qui doivent être conservés; sinon, ils peuvent forger des preuves.La conversion du code en contenu provisible nécessite la compilation du code en une série de systèmes de contrainte polynomiale.Au début, cela doit être fait manuellement, ce qui prend du temps et sujet aux erreurs.Les progrès dans ce domaine tentent d’éliminer certains des problèmes majeurs:

1. Il y a des provers plus efficaces.

2. Réduire le nombre de prétraitements.

3. Paramètres avec des circuits généraux plutôt que spécifiques.

4. Évitez les paramètres de confiance.

5. Développer des méthodes pour décrire les circuits dans des langues de haut niveau, plutôt que d’écrire des contraintes polynomiales manuellement.

Pinocchio (2013)

Pinocchio^{[15]est le premier ZK-Snark pratique et utilisable.Snark est basé sur un programme arithmétique quadratique (QAP).La taille de preuve est initialement de 288 octets.La chaîne d’outils de Pinocchio fournit un compilateur du code C aux circuits arithmétiques, en outre converti en QAP.Le protocole nécessite que le vérificateur génére des clés spécifiques au circuit.Il utilise l’appariement de courbe elliptique pour vérifier l’équation.Prouver que l’asymptocité de la génération et des paramètres clés est linéairement liée à la taille du calcul, et le temps de vérification est liné à la taille de l’entrée et de la sortie communes.}

Groth 16 (2016)

Grotter^{[16]Un nouvel argument de connaissances avec des performances améliorées a été introduite[17], utilisé pour décrire le problème des R1C.Il a la plus petite taille de preuve (seulement trois éléments de groupe) et la validation rapide, impliquant trois accords.Il s’agit également d’une étape de prétraitement pour obtenir une chaîne de référence structurée.L’inconvénient principal est qu’il nécessite différents paramètres de confiance pour chaque programme que nous voulons prouver, ce qui est gênant.Groth16 est utilisé par Zcash.}

Bulletproofs & amp;

Une faiblesse des PC KZG est qu’elle nécessite un paramètre de confiance.Bootle et al.^{[18]Un système d’argumentation efficace de connaissance zéro qui satisfait la relation du produit interne est introduit.L’argument du produit intérieur a un prover linéaire, une communication logarithmique et une interaction, mais une vérification du temps linéaire.Ils ont également développé un système d’engagement polynomial qui ne nécessite pas de paramètres de confiance.Le schéma d’engagement polynomial (PCS) utilisant ces idées a été utilisé par Halo 2 et Kimchi.}

Sonic, Marlin et Plonk (2019)

Sonique^{[19], Plonk[20]et marlin[vingt-et-un]Aborde le problème où chaque programme que nous rencontrons dans GROTH16 nécessite des paramètres de confiance en introduisant des chaînes de référence structurées communes et à la mise à jour.Marlin fournit un système de preuve basé sur R1CS (système de contraintes de rang) qui est au cœur de l’ALEO.}

Pinard^{[Vingt-deux]Un nouveau schéma arithmétique (plus tard appelé Plonkish) a été introduit et une vérification du grand produit a été utilisée pour vérifier les contraintes de réplication.Plonkish permet également l’introduction de portes spécialisées pour certaines opérations, soi-disant portes personnalisées.Plusieurs projets ont des versions personnalisées de Plonk, notamment Aztec, ZK-Sync, Polygon Zkevm, Mina’s Kimchi, Plonky2, Halo 2 et Scroll, entre autres.}

Lookups (2018/2020)

Gabizon et Williamson introduisent PLOokup en 2020^{[vingt-trois], utilisez des vérifications de macro-produits pour prouver qu’une valeur est contenue dans un tableau de valeur pré-calculé.Bien que les paramètres de recherche étaient auparavant à Arya[vingt-quatre]Cependant, cette construction nécessite de déterminer la multiplicité de la recherche, ce qui rend la construction suffisamment inefficace.Plonkup[25]Le document montre comment introduire des paramètres de plats dans PLONK.Le problème avec ces paramètres de recherche est qu’ils obligent le prover à payer l’ensemble du tableau sans égard au nombre de recherches.Cela signifie que le coût des grandes tables est assez important, et les gens ont fait beaucoup d’efforts pour réduire le coût du prover qui ne paie que le nombre de recherches qu’il utilise.Haböck présente la logup[26], qui convertit la vérification du grand-produit en somme de l’inverse à l’aide d’un dérivé du journal.Logup pour Polygon Zkevm[27]Les performances en eux sont essentielles, ils doivent diviser toute la table en plusieurs modules frappés.Ces modules doivent être correctement liés, la recherche de table croisée applique cela.Présentation de LogUp-GKR[28]Utilisez le protocole GKR pour améliorer les performances de LogUp.Calfater[29]est le premier schéma pour prouver le temps sous-linéaire avec la taille du tableau, en utilisant le temps de prétraitement O (NLOGG) et le stockage O (n), où n est la taille de la table.Plusieurs autres options ont suivi, comme Baloo[30], Flookup[31], CQ[32]et calfeutrage +[33].Lasso[34]Plusieurs améliorations sont proposées pour éviter de commettre un tableau lorsqu’il a une structure donnée.De plus, le prover de Lasso ne paie que pour les entrées de table accessibles par l’opération de recherche.Secousse[35]Utilisez Lasso pour prouver l’exécution de la machine virtuelle via des recherches.}

Spartan (2019)

spartiate^{[36]Un IOP (« Interactive Oracle Preuve ») est fourni pour le circuit décrit à l’aide de R1CS, en utilisant les propriétés des polynômes multivariés et le protocole Sumcheck.En utilisant un schéma d’engagement polynomial approprié, il produit un snark transparent à preuves linéaire.}

Hyperplonk (2022)

Hyperplonk^{[37]Sur la base de l’idée de PLONK, des polynômes multivariés sont utilisés.Il s’appuie sur le protocole Sumcheck plutôt que sur le quotient pour vérifier l’exécution des contraintes.Il prend également en charge les contraintes d’ordre élevé sans affecter le temps d’exécution du prover.Puisqu’il s’appuie sur des polynômes multivariés, il n’est pas nécessaire d’effectuer FFT, et le temps d’exécution du prover est linéairement lié à la taille du circuit.Hyperplonk introduit une nouvelle PIO de permutation pour les champs plus petits et un protocole d’ouverture par lots basé sur Sumcheck qui réduit le travail de Prover, la taille de la preuve et le temps de validateur.}

Schémas de pliage (2008/2021)

Nova^{[38]Le concept d’un schéma de pliage est introduit, qui est une nouvelle méthode pour implémenter l’informatique progressivement vérifiable.Le concept d’IVC peut être retracé à Valiant[39], Il montre comment combiner deux preuves de longueur k en une seule preuve de longueur k.L’idée est que nous pouvons prouver que l’exécution de l’étape I à l’étape I +1 est correcte en preuve récursive que la transformation de l’étape I – 1 à l’étape I est correcte, tout calcul de longue date.Nova gère bien l’informatique unifiée;[40].Nova utilise une version détendue de R1CS et travaille sur des courbes elliptiques amicales.IVC est implémenté à l’aide de boucles conviviales (telles que les courbes de pâtes) et est également utilisée comme élément constitutif principal de la mise en œuvre de l’état concis des cornichons, Mina.Cependant, le concept de pliage est différent de la vérification récursive du snark.}

L’idée d’accumulateur est plus profondément connectée au concept de preuve par lots.Halo^{[41]Le concept d’accumulation est introduit comme alternative aux combinaisons de preuves récursives.Protostar[42]Fournit une solution IVC non uniforme pour PLONK, soutenant les portes et les recherches de vecteur de haut niveau.}

Utilisation de la fonction de hachage anti-collision

Pendant que Pinocchio se développait, il y avait quelques idées pour générer des schémas de circuit / arithmétiques qui pourraient prouver correctement l’exécution des machines virtuelles.Même si l’arithmétique du développement de machines virtuelles peut être plus complexe ou moins efficace que d’écrire des circuits dédiés pour certains programmes, son avantage est qu’il peut prouver n’importe quel programme complexe en démontrant que le programme est exécuté correctement dans la machine virtuelle.L’idée dans Tinyram est ensuite améliorée par la conception de la machine virtuelle du Caire et des machines virtuelles ultérieures telles que ZK-EVM ou ZKVMS à usage général.L’utilisation d’une fonction de hachage résistante à une collision élimine le besoin de paramètres de confiance ou d’opérations de courbe elliptique, mais au prix de la preuve s’allonge.

Tinyram (2013)

En morts pour c^{[43]Dans cet article, ils ont développé un snark basé sur PCP pour prouver l’exactitude de l’exécution du programme C, qui est compilé en Tinyram, qui est un ordinateur d’instructions mince.}

Remarque: PCP, probabilité de preuve à vérification probabiliste.Contrairement aux systèmes de preuve traditionnels où les vérificateurs doivent vérifier l’ensemble de la preuve, le PCP ne nécessite qu’un aléatoire limité pour permettre une vérification efficace.

L’ordinateur adopte une structure de Harvard avec une mémoire aléatoire qui est adressable au niveau des octets.En utilisant le non-déterminisme, la taille du circuit est presque linéairement liée à la taille calculée, et toutes les boucles liées aux données, les flux de commande et l’accès à la mémoire peuvent être gérés efficacement.

Starks (2018)

Étoiles^{[44]Proposé en 2018 par Ben Sasson et al.Ils implémentent des tailles de preuve de 0 (log ^ 2 n), ont un prover et un validateur rapides, ne nécessitent pas de configuration de confiance et sont supposés être une sécurité post-quantitum.Ils sont utilisés par Starkware / StarkNet pour la première fois, avec Cairo VM.Ses principales introductions incluent la représentation intermédiaire algébrique (AIR) et les protocoles FRI[45](Fast Reed-Solomon Interactive Oracle Preuve de proximité).Il est également utilisé par d’autres projets (Polygon Miden, Risc0, Winterfell, Neptune), ou a vu quelques adaptations de composants (Boojum, Plonky2, Starky de ZK-Sync).}

Ligero (2017)

Lige^{[46]Un système de preuve est proposé pour implémenter une taille de preuve d’O (√n), où n est la taille du circuit.Il organise des coefficients polynomiaux sous forme de matrice et utilise des codes linéaires.Fusée[47]S’appuyant sur Ligero, le concept de régimes d’engagement polynomial indépendant du domaine a été introduit.}

Quelques nouveaux développements

L’utilisation de différents systèmes de preuve dans la production montre les avantages de chaque méthode et entraîne de nouveaux développements.Par exemple, l’arithmétique Plonkish fournit un moyen facile d’inclure des portes personnalisées et des arguments de recherche;De même, l’utilisation de la vérification des macroproductions dans l’air (air randomisé qui apporte un prétraitement) améliore ses performances et simplifie les paramètres d’accès à la mémoire.La promesse des fonctions de hachage est devenue populaire en raison de sa vitesse de matériel ou de l’introduction de nouvelles fonctions de hachage pour Snark.

Nouveau système d’engagement polynomial (2023)

Avec l’émergence de SNACKS efficaces basés sur des polynômes multivariés, tels que Spartan ou Hyperplonk, il y a eu un plus grand intérêt pour de nouveaux schémas d’engagement qui s’appliquent à de tels polynômes.Binius^{[48]Zéromorphe[49]et pliage de base[50]Tous proposent de nouvelles formes d’engagement envers les polynômes multilinéaires.Binius a l’avantage de ne pas avoir de frais généraux supplémentaires lorsqu’il indique des types de données (tandis que de nombreux systèmes de preuve utilisent au moins des éléments de champ 32 bits pour représenter des bits uniques) et peuvent fonctionner sur des domaines binaires.Le schéma d’engagement utilise une ligne de freinage conçue à des fins indépendantes sur le terrain.Basefold favorise FRI à des codes autres que Reed-Solomon, apportant un PC indépendant du domaine.}

Remarque indépendant du domaine: Dans un schéma d’engagement polynomial indépendant du domaine, le processus d’engagement ne dépend pas de propriétés spécifiques d’un domaine particulier.Cela signifie que des engagements peuvent être pris envers les polynômes de toute structure algébrique, tels que des domaines finis, des courbes elliptiques et même des anneaux entiers.

Système de contrainte personnalisable (2023)

CCS^{[51]R1CS généralisés, tout en capturant R1CS, Plonkish et Arithmetics Air, sans frais généraux supplémentaires.L’utilisation de CCS en conjonction avec Spartan IOP produit un superspartan, qui prend en charge les contraintes et les provers de dimensions ne doivent pas supporter le coût cryptographique qui évolue à mesure que les métriques des contraintes augmentent.En particulier, Superspartan fournit de l’air avec un snark linéaire à l’épreuve du temps.}

en conclusion

Cet article décrit les progrès des SNARKS depuis le milieu des années 80.Les progrès de l’informatique, des mathématiques et du matériel et de l’introduction de la blockchain ont conduit à l’émergence de SNARKS nouveaux et plus efficaces, ouvrant la porte à de nombreuses applications qui peuvent changer notre société.Les chercheurs et les ingénieurs ont proposé des améliorations et des adaptations aux SNACK en fonction de leurs besoins, en se concentrant sur la taille de la preuve, l’utilisation de la mémoire, les paramètres transparents, la sécurité post-sur-quanttum, le temps de preuve et le temps de vérification.Bien qu’il y ait initialement eu deux lignes principales (Snarks vs Starks), les limites entre les deux ont commencé à disparaître, tentant de combiner les avantages de différents systèmes de preuve.Par exemple, une combinaison de différents schémas arithmétiques avec de nouveaux schémas d’engagement polynomial.Nous pouvons nous attendre à ce que de nouveaux systèmes de preuve continuent d’émerger et que les performances s’améliorent, et il sera difficile pour certains systèmes qui prennent un certain temps à s’adapter pour suivre ces développements, sauf si nous pouvons facilement utiliser ces outils sans modifier une infrastructure de base.

Références

[1] Lien: https://blog.lambdaclass.com/our-highly-subjective-view-on-the-history-of-zero-knowledge-profts/

[2] Plan de traduction des liens: https://github.com/lbc-team/pioneer

[3] Équipe de traduction: https://learnblockchain.cn/people/412

[4] Tiny Bear: https://learnblockchain.cn/people/15

[5] Learnblockchain.cn/article…: https://learnblockchain.cn/article/7422

[6] Article: https://blog.lambdaclass.com/transforming-the-future-with-zero-knowledge-profts-ly homomorphic-cryption-and-new-distributed-syst EMS-algorithms /

[7] L’éclosion du Cambrien de preuve de cryptage: https://medium.com/starkware/cambrian-explosion-of-criptographic-profts-5740a41cdbd2?ref=blog.lambdaclass.com

[8] La vidéo suivante: https://www.youtube.com/watch?v=uchjtilpzfo&ref=blog.lambdaclass.com

[9] Protocole Sumcheck: https://blog.lambdaclass.com/have-you-checked-your-sums/

[10] Lund, Fortnow, Karloff et Nisan: https://dl.acm.org/doi/pdf/10.1145/146585.146605?ref=blog.lambdaclass.com

[11] Protocole GKR: https://www.microsoft.com/en-us/research/wp-content/uploads/2016/12/2008-delegatingcomputation.pdf?ref=blog.lambdaclass.com

[12] Kate, Zaverucha et Goldberg: https://www.iacr.org/archive/asiacrypt2010/6477178/6477178.pdf?ref=blog.lambdaclass.com

[13] EIP-4844: https://github.com/ethereum/eips/blob/master/eips/eip-4844.md?ref=blog.lambdaclass.com

[14] Mina-Ethereum Bridge: https://blog.lambdaclass.com/mina-to-ethereum-bridge/

[15] Pinocchio: https://eprint.iacr.org/2013/279?ref=blog.lambdaclass.com

[16] Groth: https://eprint.iacr.org/2016/260.pdf?ref=blog.lambdaclass.com

[17] Nouvel argument de connaissance avec des performances améliorées: https://blog.lambdaclass.com/groth16/

[18] Bootle et al .: https://eprint.iacr.org/2016/263?ref=blog.lambdaclass.com

[19] Sonic: https://eprint.iacr.org/2019/099?ref=blog.lambdaclass.com

[20] Plonk: https://eprint.iacr.org/2019/953?ref=blog.lambdaclass.com

[21] Marlin: https://eprint.iacr.org/2019/1047?ref=blog.lambdaclass.com

[22] Plonk: https://blog.lambdaclass.com/all-you-wanted-to-know-about-plonk/

[23] PLookup: https://eprint.iacr.org/2020/315?ref=blog.lambdaclass.com

[24] Arya: https://eprint.iacr.org/2018/380?ref=blog.lambdaclass.com

[25] Plonkup: https://eprint.iacr.org/2022/086?ref=blog.lambdaclass.com

[26] Logup: ​​https://eprint.iacr.org/2022/1530?ref=blog.lambdaclass.com

[27] Polygon zkevm: https://toposware.medium.com/beyond-limits-pushing-the-boundaires-of-zk-evm-9dd0c5ec9fca?ref=blog.lambdaclass.com

[28] Logup-gkr: https://eprint.iacr.org/2023/1284?ref=blog.lambdaclass.com

[29] Caloulk: https://eprint.iacr.org/2022/621?ref=blog.lambdaclass.com

[30] Baloo: https://eprint.iacr.org/2022/1565?ref=blog.lambdaclass.com

[31] Flookup: https://eprint.iacr.org/2022/1447?ref=blog.lambdaclass.com

[32] CQ: https://eprint.iacr.org/2022/1763?ref=blog.lambdaclass.com

[33] Cauflk +: https://eprint.iacr.org/2022/957?ref=blog.lambdaclass.com

[34] lasso: https://eprint.iacr.org/2023/1216?ref=blog.lambdaclass.com

[35] Jolt: https://eprint.iacr.org/2023/1217?ref=blog.lambdaclass.com

[36] Spartan: https://eprint.iacr.org/2019/550?ref=blog.lambdaclass.com

[37] Hyperplonk: https://eprint.iacr.org/2022/1355.pdf?ref=blog.lambdaclass.com

[38] Nova: https://eprint.iacr.org/2021/370?ref=blog.lambdaclass.com

[39] Valiant: https: //https//iacr.org/archive/tcc2008/49480001/49480001.pdf? Ref = blog.lambdaclass.com

[40] Supernova: https://eprint.iacr.org/2022/1758?ref=blog.lambdaclass.com

[41] Halo: https://eprint.iacr.org/2019/1021.pdf?ref=blog.lambdaclass.com

[42] Protostar: https://eprint.iacr.org/2023/620?ref=blog.lambdaclass.com

[43] Scarks pour C: https://eprint.iacr.org/2013/507?ref=blog.lambdaclass.com

[44] Starks: https://eprint.iacr.org/2018/046?ref=blog.lambdaclass.com

[45] Protocole FRI: https://blog.lambdaclass.com/how-to-code-fri-from-scratch/

[46] LIGERO: https://eprint.iacr.org/2022/1608?ref=blog.lambdaclass.com

[47] Brakedown: https://eprint.iacr.org/2021/1043?ref=blog.lambdaclass.com

[48] ​​Binius: https://blog.lambdaclass.com/snarks-on-binary-fields-binius/

[49] Zeromorph: https://eprint.iacr.org/2023/917?ref=blog.lambdaclass.com

[50] Basefold: https://blog.lambdaclass.com/how-does-basefold-polynomial-commitment-scheme-generalize-fri/

[51] CCS: https://eprint.iacr.org/2023/552?ref=blog.lambdaclass.com

[52] DECERT.ME: https://decert.me/