Vitalik: Support decentralized staking with more anti-related incentives

Author: Vitalik Buterin, @vitalik.eth; Compiled by: Songxue, Bitchain Vision

One strategy for better decentralization in incentive protocols is punishment for relevance.That is, if one participant behaves improperly (including accidents), the more other participants (measured by total ETH) who behave improperly with them, the greater the punishment they will be.The theory holds that if you are a large participant, any mistakes you make are more likely to be copied in all “identities” you control, even if you spread your tokens into many nominally independent accounts.

This technology has been applied in the Ethereum cut (and, arguably, inactive leak) mechanism.However, edge-case incentives that occur only in extremely special attacks may never appear in practice,Probably not enough to inspire decentralization.

This article suggests extending similar anticorrelation incentives to more “trivial” failure cases, such as missing proofs, which almost all validators do at least occasionally.The theory suggests that larger stakers, including wealthy individuals and staking pools, will run many validators on the same internet connection or even on the same physical computer, which will result in disproportionately related failures.Such stakers can always make separate physical settings for each node, but if they end up doing so, it means we have completely eliminated the economies of scale of staking.

Solidity check: Are errors from different validators in the same “cluster” actually more likely to be associated with each other?

We can check this by combining two datasets: (i) proof data from recent periods, showing which validators should be proven during each slot, and which validators actually proven, and (ii)Map the validator ID to a cluster containing many validators (such as “Lido”, “Coinbase”, “Vitalik Buterin”).You canHere,HereandHereFind the dump of the former, inHereFind the latter’s dump.

We then run a script to calculate the total number of common failures: two instances of validators in the same cluster are assigned to prove in the same time slot and fail in that time slot.

We also calculate the expectedCommon fault:If the failure is a total result of random chance, then the number of common failures that should occur.

For example, suppose there are 10 validators, one of the cluster size is 4, the others are independent, and 3 validators fail: two are inside the cluster and one is outside the cluster.

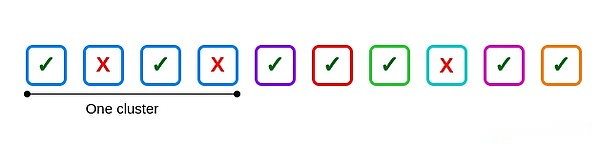
Here is a common failure: the second and fourth validators in the first cluster.If all four validators in the cluster fail, six common failures occur, one for every six possible pairs.

But how many common failures should be made?This is a tough philosophical question.Several ways to answer:

For each failure, assume that the number of common failures is equal to the failure rate of other validators in that slot multiplied by the number of validators in the cluster and cut it in half to compensate for the repeated calculations.For the example above, 2/3 is given.

Calculate the global failure rate, squared, and multiply by [n*(n-1)]/2 for each cluster.This is given [(3/10)^2]*6=0.54

Redistribute each validator’s failures randomly across its entire history.

Each method is not perfect.The first two methods fail to consider different clusters with different quality settings.At the same time, the last method fails to take into account the correlations arising from different time slots with different inherent difficulties: for example, time slot 8103681 has a large number of proofs that are not included in a single time slot, possibly because the block hasPosting is exceptionally late.

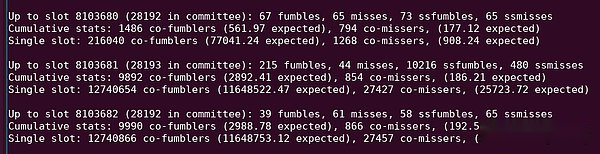
See “10216 ssfumbles” in this python output.

I ended up implementing three methods: the first two above, and a more complex approach, I compared “actual co-failure” with “fake co-failure”: each cluster member is replaced with (pseudo)randomThe failure of the validator has a similar failure rate.

I’ve also clearly distinguishedMistakesandmiss.My definition of these terms is as follows:

Mistakes: When the verifier misses the proof in the current period, but correctly proves in the previous period;

miss: When the verifier missed the proof in the current period and also missed the proof in the previous period.

The goal is to distinguish two distinct phenomena: (i) network failure during normal operation, and (ii) offline or long-term failure.

I also do this analysis on two datasets at the same time: the maximum deadline and the single slot deadline.The first dataset treats the validator as failing within a period of time only if the proof is not included at all.If the proof is not included in a single slot, the second dataset treats the validator as a failure.

Here are the results of my first two methods of calculating expected common failures.SSfumbles and SSmisses here refer to goals and mistakes that use a single-slot dataset.

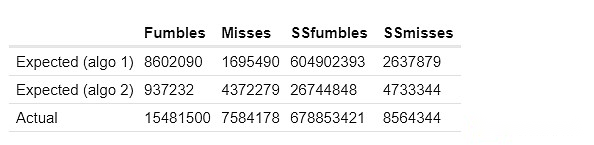
For the first approach, the actual behaviors differ because for efficiency, a more restricted dataset is used:

The “Expected” and “Fake Cluster” columns show how many common failures “should” be in the cluster based on the above techniques.The Actual column shows how many common failures actually exist.Consistently, we see strong evidence of “too many correlation failures” within the cluster: two validators in the same cluster are significantly more likely to miss proofs at the same time than two validators in different clusters.

How do we apply it to the penalty rules?

I make a simple argument: In each slot, let p divide the number of slots currently missed by the average of the last 32 slots.

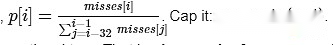
The penalty for proof of this slot should be proportional to p.

That is to say,Compared to other recent slots, the penalty for not proven to be proportional to the number of failed validators in that slot.

There is a good feature of this mechanism, that is, it is not easy to attack: in any case, failure reduces your penalties, and manipulating the average is enough to have an impact that requires you to make a lot of failures yourself.

Now, let’s try to actually run it.Here are the total penalty for large clusters, medium clusters, small clusters, and all validators (including non-clusters):

Basic:One point is deducted for each mistake (that is, similar to the current situation)

basic_ss:Same, but need to include a single slot to be considered a miss

Exceeded:Use the p calculated above to punish the p point

extra_ss:Use the p calculated above to punish the p point, requiring a single slot to contain no miss

Using the “basic” scheme, large schemes have about 1.4 times the advantage over small schemes (about 1.2 times in single-slot datasets).Using the “extra” scheme, the value dropped to about 1.3 times (about 1.1 times in a single-slot dataset).Through multiple other iterations, using slightly different data sets, the excess penalty scheme uniformly narrows the advantages of “big people” over “little people”.

What’s going on?

There are very few failures per slot: usually only a few dozen.This is much smaller than almost any “large share”.In fact, it is less than the number of validators active in a single slot than the large stakers (i.e. 1/32 of their total stock).If a large staker runs many nodes on the same physical computer or internet connection, any failure could affect all of its validators.

This means:When large validators show proof-inclusion failures, they will single-handedly change the failure rate of the current slot, which in turn will increase their penalty.Small validators don’t do this.

In principle, major shareholders can bypass this punishment scheme by placing each validator on a separate internet connection.But this sacrifices the economies of scale advantage that large stakeholders can reuse the same physical infrastructure.

Further analysis

• Look for other strategies to confirm the magnitude of this effect, where validators in the same cluster are likely to fail at the same time.

• Try to find an ideal (but still simple to avoid overfitting and unutilization) reward/punishment scheme to minimize the average advantage of large validators over small validators.

• Try to demonstrate the security nature of such incentive schemes, ideally identifying a “design space area” where the risk of a strange attack (e.g., strategically offline at a specific time to manipulate the average) is too expensive and not worth it.

• Cluster by geographical location.This can determine whether the mechanism can also inspire geographical decentralization.

• Clustering through (execution and beacon) client software.This can determine whether the mechanism can also incentivize the use of a small number of customers.