Author: Andrey Sergeenkov, CoinTelegraph; Compiled by: Deng Tong, Bitchain Vision
1. Understand the bond curve in DeFi
In Decentralized Finance (DeFi), the bond curve uses smart contracts and mathematical formulas to adjust its price dynamically based on the supply of tokens.
The bond curve is a smart contract that determines the price of the token based on the token’s circulation supply algorithm.As more tokens are purchased, the price is raised, and when the tokens are sold or removed from circulation, the price is down.
This automatic pricing mechanism ensures liquidity of new tokens without the need for traditional order books or external liquidity providers.It is achieved by smart contracts that embed liquidity directly into tokens.
Specifically,The bond curve utilizes the principle of supply and demand economy.When the demand for tokens increases (reflected by purchase increase), smart contracts increase prices accordingly.Smart contracts lower prices when selling activity indicates a decrease in demand.
This dynamic adjustment is based on a predefined curve that simulates the relationship between price and supply.Therefore, the bond curve allows automated, decentralized liquidity that responds to real-time market conditions.
2. Price determination in the bond curve
The bond curve in DeFi adjusts token prices based on supply, supporting various economic strategies and market dynamics.
Through mathematical modeling, projects can customize bond curve economics by defining unique curves, thus determining how token prices change according to their supply.In theory, there is no limit to the type of curve, but the most common forms include:
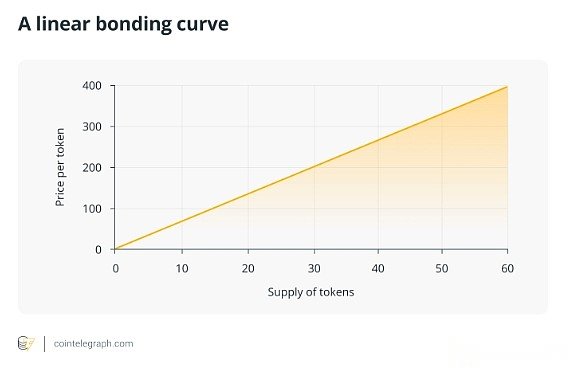
Linear curve
The linear bond curve is a simple mathematical model in which the price of tokens increases proportional to the number of tokens sold.In this model, each additional coin or token sold will increase the price by a fixed, predetermined amount.
Below is a simple graphical representation of a linear curve, where the X-axis (horizontal) represents the supply of tokens and the Y-axis (vertical) shows the price of each token at that supply level.
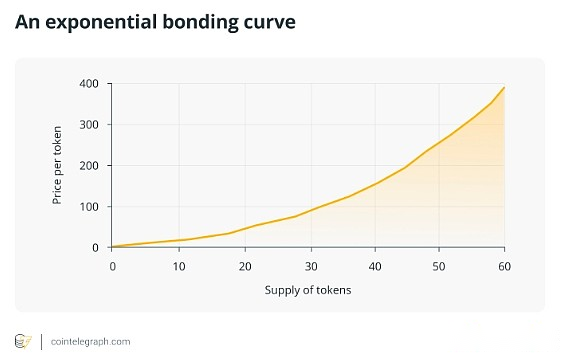
Exponential curve
The index curve makes the price of the token exponentially dependent on supply.This means that if the supply doubles, the price will exceed double.Even adding a few tokens can lead to a sharp rise in prices.This makes the token price rise faster.
These curves reward early buyers to the greatest extent possible.When demand increases later, initial users will likely sell their tokens for a higher price.Therefore, the index curve is perfect for projects that want to encourage early participation.The initial users take the greatest risk, but if the project is successful, they can make the most profit.
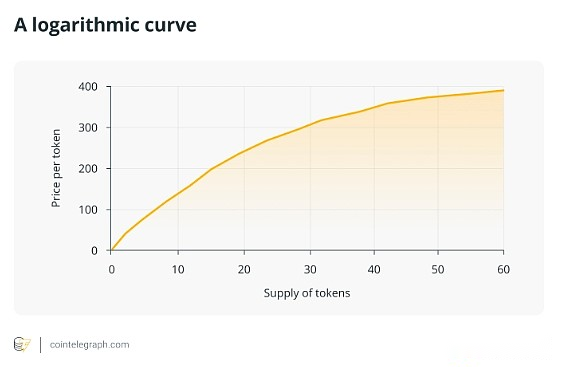
Logarithmic curve
The logarithmic curve causes the token price to rise rapidly as more tokens increase.But as supply continues to expand, the price growth rate gradually slows down.Therefore, prices will rise sharply at the beginning, but will stabilize over time.This maximizes early investors, as their tokens will quickly increase in value in the early stages.Fast early-stage profit potential can attract the first buyers to provide liquidity.
In DeFi, in addition to linear, exponential and logarithmic models, there are a variety of bond curve types to choose from.For example, there are S-curves for phased growth and stability, Step curves for milestone-based price growth, and reverse curves for lowering prices as supply grows, each for a specific bond curve economyThe results and project goals were customized.
3. Application of bond curve in cryptocurrency
The bond curve provides automated token liquidity and dynamic pricing for projects, transactions, stablecoins, communities and governance.
The bond curve serves as the basic mechanism for automatic liquidity startup in the initial decentralized exchange issuance (IDO), allowing projects to launch new tokens by dynamically adjusting liquidity pool reserves.This model is different from traditional order books, ensuring continuous and algorithmic adjustments to liquidity based on real-time demand.The flexibility of dynamic pricing in blockchain, implemented by the bond curve, creates new possibilities for token distribution and trading.
Platforms like Uniswap and Curve use the bond curve for independent market makers, enhancing liquidity and providing more efficient trading for various tokens, especially those that may be affected by low liquidity.
The bond curve plays a key role in the stablecoin protocol, establishing currency reserves and maintaining fixed prices through algorithmic supply adjustments, ensuring that these digital currencies are stable in a fully decentralized manner.However, this approach is risky, as algorithmic stablecoins rely solely on bond curves and programmatic supply changes to maintain their fixed price.
For example, the algorithmic stablecoin TerraUSD (UST) lost its fixed price of 1:1 with the US dollar after a dramatic run in May 2022.This shows that decentralized algorithmic stablecoins still have stability challenges compared to asset-support models.
When demand drops sharply, algorithmic stablecoins may not be able to quickly adjust supply to maintain their fixed price.Therefore, while the bond curve allows for a decentralized stabilization mechanism, they have not yet fully demonstrated sufficient resilience to runs compared to mortgage alternatives.
The bond curve facilitates a continuous token model in DeFi that allows automatic liquidity start, autonomous market makers and dynamic pricing adjusted to real-time demand.
They play a key role in decentralized autonomous organizations (DAO) governance, buying voting tokens through the bond curve, aligning investment with governance participation, and ensuring pricing reflects the level of commitment to DAO.
4. Decentralized exchange (DEX) and bond curves
The bond curve provides customized, automated decentralized liquidity and pricing for various decentralized exchanges (DEXs).
Uniswap
Uniswap uses a constant product formula, a specific type of bond curve used for its automatic market makers (AMM) protocol.This formula ensures liquidity by maintaining the product of the two assets in any given liquidity pool.For example, if the pool contains Ethereum (ETH) and another token, the product of their quantity remains constant, and the price is determined based on supply and demand dynamics.This approach provides continuous liquidity and price discovery without the need to use a traditional order book.
Curve Finance
Curve Finance in DeFi focuses on stablecoins and adopts a bond curve specifically targeting assets that are expected to have equal value.Its bond curve is designed to reduce slippage and maintain stable prices for closely pegged assets such as different stablecoins pegged to the dollar.For asset pairings with similar values, the curve is flatter, which reduces the impact of transactions on price changes and makes it more efficient for exchanges between stablecoins.
Balancer
Balancer uses a generalized version of the constant product formula, allowing custom liquidity pools where up to eight assets can be composed of any weighted proportion.This flexibility allows users to create their own automatic balanced portfolio and liquidity pools and use custom bond curves to define the relationship between asset prices and quantity of pools.Balancer’s approach extends the utility of the bond curve beyond the two asset pools, houses a wider range of trading strategies and portfolio management practices.
5. Challenges Facing to Implementing the Bond Curve
Challenges to the bond curve include modeling, security and legal issues that require extensive testing, auditing and compliance analysis to properly design, deploy and regulate automated token pricing systems.
Designing appropriate curve shapes that align with incentive mechanisms and encourage expected market behavior requires extensive modeling and testing.For example, a curve that is too steep or smooth may lead to price manipulation.
The security of smart contracts that execute bond curves must be audited to prevent exploits that may affect price integrity.In addition, smart contracts need to be optimized to minimize gas costs for automatic transactions.
Ensuring the security of smart contracts that manage the bond curve is critical, as vulnerabilities can lead to arbitrage or manipulation.Formal verification, vulnerability bounties and audits help reduce this risk.Ongoing research focuses on implementing dynamic curves that can be algorithmically adjusted according to market conditions.
The legal regulatory issue of the bond curve remains an open question.Most jurisdictions have not yet clearly directed whether automatic market makers (such as bond curves) constitute a regulated trading venue or securities issuance.
Projects must carefully analyze the rights granted by tokens sold through the bond curve based on different jurisdictions.Local regulations related to crypto assets and securities vary across regions.
For example, if the token grants holders the rights to profit, governance, etc., it may be considered a securities in some jurisdictions and requires compliance with relevant securities regulations.
However, other jurisdictions may be more flexible in classifying practical tokens, even if these tokens have the accompanying profit or governance rights.Therefore, the project should review the regulations of its target market.
Many projects adopt a practical token model, where tokens only provide access to the project’s products or services, and holders have no profit rights or governance capabilities.In many cases, such restricted token design avoids meeting the legal definition of securities.
However, even purely practical tokens may still apply to Know Customer (KYC) and Anti-Money Laundering (AML) regulations.These regulations require verification of user identity and source of funding.
Projects must seek legal advice to address this complex legal environment.Legal regulatory issues for crypto tokens are evolving in various jurisdictions.Ongoing legal developments may provide a clearer framework for designing regulatory-compliant token implementation and bond curve systems.