
オリジナルタイトル:vitalik Buterinによって書かれた「サークルスタークスの探索」、Chris、Techub Newsによって編集されたEthereumの共同設立者
この記事を理解する前提は、あなたがすでに嗅覚とスタークの基本原則を理解していることです。これに慣れていない場合は、この記事の最初のいくつかの部分を読んで基本を学ぶことをお勧めします。
近年、Starksプロトコル設計の傾向は、より小さなフィールドの使用に移行することです。初期のStarks制作の実装では、256ビットフィールドを使用しました。これは、大量のモジュール操作(21888 … 95617など)であり、これらのプロトコルが楕円曲線ベースのシグネチャと互換性がありました。ただし、この設計は比較的非効率的です。一般的には、これらの多数の処理と計算は実用的な目的はありません。計算時間の9分の1のみが必要です。この問題を解決するために、Starksはより小さなフィールドに変わり始めました:最初のGoldilocks、次にMersenne31とBabybear。
このシフトは、StarkwareがM3ラップトップで1秒あたり620,000 Poseidon2ハッシュを証明する能力など、証明速度を向上させます。これは、Poseidon2をハッシュ関数として信頼する意思がある限り、効率的なZK-EVMを開発する際の問題を解決できることを意味します。では、これらのテクノロジーはどのように機能しますか?これらの証明は、より小さなフィールドでどのように確立されますか?これらのプロトコルは、Biniusのようなソリューションと比較してどうですか?この記事では、これらの詳細については、Circle Starks(STWOのSTWO、PolygonのPlonky3、およびMersenne31フィールドと互換性のある一意のプロパティを備えた独自のバージョンと呼ばれるスキームに焦点を当てています。
小さな数学フィールドを使用する場合の一般的な問題
ハッシュベースの証明(またはあらゆる種類の証明)を作成する場合、非常に重要な手法は、ランダムなポイントでの多項式の評価結果を証明することにより、多項式の特性を間接的に検証することです。ランダムなポイントでの評価は、通常、多項式全体に対処するよりもはるかに簡単であるため、このアプローチは証明プロセスを大幅に簡素化できます。
たとえば、証明システムが多項式のコミットを生成する必要があると仮定します。Aは、a^3(x) + x -a(\ omega*x)= x^n(zk -snarkの非常に一般的なものを満たす必要がありますプロトコル証明タイプ)。プロトコルは、ランダム座標を選択し、A(r) + r -a(\ omega*r)= r^nを証明できます。次に、a(r)= cを反転させ、q = \ frac {a -c} {x -r}が多項式であることを証明します。
プロトコルまたは内部メカニズムの詳細を事前に理解している場合、これらのプロトコルをバイパスまたはクラックする方法を見つけることができます。これを達成するために、特定の操作または方法が次に言及される場合があります。たとえば、A(\ omega * r)方程式を満たすために、a(r)を0に設定してから、これら2つのポイントを通過する直線を作成できます。
これらの攻撃を防ぐために、攻撃者がAを提供した後にRを選択する必要があります(Fiat-Shamirはプロトコルセキュリティを強化するために使用される技術です。これは、特定のハッシュ値に特定のパラメーターを設定することで攻撃を回避します。攻撃者がこれらのパラメーターを予測または推測できないように設定し、それによりシステムのセキュリティが改善されます。
2019年の楕円曲線ベースのプロトコルとスタークでは、この問題は簡単です。すべての数学は256ビットの数字で実行されるため、Randance 256ビット数としてRを選択できるため、今すぐ実行できます。ただし、小さなフィールドのスタークでは問題があります。選択できるR値は約20億のR値しかありません。そのため、ワークロードが高いにもかかわらず、証明を策定したい攻撃者は20億回しか試みません。しかし、決定された攻撃者にとって、それはまだできます!
この問題には2つの解決策があります。
-
複数のランダムチェックを実行します
-
拡張フィールド
複数のランダムチェックを実行する最も簡単で効果的な方法:1つの座標をチェックする代わりに、4つのランダム座標を繰り返し確認することをお勧めします。これは理論的に実現可能ですが、効率の問題があります。特定の値よりも少ない程度の多項式を扱っていて、特定のサイズのドメインで動作する場合、攻撃者は実際にこれらの位置で正常に見える悪意のある多項式を構築できます。したがって、プロトコルを正常に破ることができるかどうかは確率的な問題であるため、全体的なセキュリティを強化し、攻撃者に対する効果的な防御を確保するために、チェックのラウンド数を増やす必要があります。
これは別のソリューションにつながります。拡張ドメイン、拡張ドメインは複数形に似ていますが、有限ドメインに基づいています。α\alphaαとして示される新しい値を導入し、α2=ある程度の値\ alpha^2 = \ text {あるvalue}α2=ある程度の値など、特定の関係を満たしていることを宣言します。このようにして、有限ドメインでより複雑な操作を可能にする新しい数学構造を作成します。この拡張ドメインでは、乗算の計算は、新しい値α\alphaαを使用した乗算になります。単一の数字だけでなく、拡張ドメインで値ペアを操作できるようになりました。たとえば、MersenneやBabyBearなどのフィールドで作業する場合、このような拡張機能により、より多くの価値の選択肢があるため、セキュリティが向上します。フィールドのサイズをさらに増やすために、同じ手法を繰り返し適用できます。α\alphaαを使用しているため、Mersenne31では、α2=α2= alpha^2 = \ text {mulation}α2= anuter valueになるようにα\alphaαを選択するものとしてマニフェストする新しい値を定義する必要があります。

コード(Karatsubaで改善できます)
ドメインを拡張することにより、セキュリティのニーズを満たすのに十分な価値があります。DDDよりも少ない程度の多項式を扱っている場合、各ラウンドは104ビットのセキュリティを提供できます。これは、十分なセキュリティがあることを意味します。128ビットなど、より高いセキュリティレベルに到達する必要がある場合は、セキュリティを強化するためにプロトコルに追加のコンピューティング作業を追加できます。
拡張ドメインは、FRI(Fast Reed-Solomon Interactive)プロトコルおよびランダムな線形組み合わせを必要とするその他のシナリオでのみ使用されます。ほとんどの数学的操作は、通常、Modulo PPPまたはQQQであるフィールドである基本フィールドで実行されています。一方、ほとんどすべてのハッシュされたデータはベースフィールドで実行されるため、各値には4バイトのハッシュがあります。そうすることで、セキュリティの強化が必要なときに大きなフィールドを使用しながら、小さなフィールドの効率を活用できます。
通常の金曜日
SnarkまたはStarkを構築するとき、最初のステップは通常、算術です。これは、任意の計算上の問題を、いくつかの変数と係数が多項式である方程式に変換するためです。具体的には、この方程式は通常、p(x、y、z)= 0p(x、y、z)= 0のように見えます。ここで、pは多項式です。 xとyの値を提供します。そのような方程式が存在すると、方程式の解は基礎となる計算問題の解に対応します。
解決策があることを証明するには、提案する価値が実際に合理的な多項式であることを証明する必要があります(分数ではなく、一部の場所では多項式のように見え、他の場所では異なる多項式などです。 、およびこれらの多項式には一定の最大度があります。これを行うには、段階的なランダムな線形コンビネーション手法を使用します。
-
多項式Aの評価値があり、その程度が2^{20}未満であることを証明したいとします
-
多項式b(x^2)= a(x) + a(-x)、c(x^2)= \ frac {a(x)-a(-x)} {x}
-
Dは、BとCのランダムな線形結合、つまりD = B+RCD = B+RCD = B+RCであり、Rはランダム係数です。
基本的に、b分離株は係数aでもありますか?BとCが与えられた場合、元の多項式A(x)= b(x^2) + xc(x^2)を復元できます。Aの程度が実際に2^{20}未満の場合、BとCの程度はそれぞれAの程度とAの程度をマイナス1になります。偶数と奇妙な用語の組み合わせが程度を増加させないためです。DはBとCのランダムな線形結合であるため、Dの程度もAの程度である必要があります。これにより、Aの程度がDの程度で要件を満たすかどうかを確認できます。
まず、FRIは、D/2の多項式度を証明する問題に対して、Dの多項式度を証明する問題を単純化することにより、検証プロセスを簡素化します。このプロセスは数回繰り返すことができ、毎回途中で問題を簡素化できます。
FRIの実用的な原則は、この単純化されたプロセスを繰り返すことです。たとえば、多項式がDであるという証拠から始めて、一連のステップを通じて、最終的に多項式がD/2であることを証明します。各単純化の後、生成された多項式の程度は徐々に減少します。ステージの出力が予想される多項式度ではない場合、このチェックラウンドは失敗します。誰かがこのテクニックを通じて程度の程度ではない多項式をプッシュしようとする場合、出力の第2ラウンドでは、程度は期待を満たさない一定の確率があり、第3ラウンドでは、より多くの可能性があります。非適合性の状況になります。この設計は、要件を満たさない入力を効果的に検出および拒否することができます。データセットがほとんどの場所で次数dを持つ多項式に等しい場合、このデータセットにはFRIによって検証される可能性があります。ただし、このようなデータセットを構築するには、攻撃者は実際の多項式を知る必要があるため、わずかな欠陥のある証明でさえ、プロバーが「実際の」証明を生成できることを示しています。
ここで何が起こっているのか、そしてこの作業を行うために必要なプロパティを詳しく見てみましょう。各ステップでは、多項式の数を半分に削減しながら、ポイントのセット(焦点を当てたポイントのセット)を半分に減らします。前者は、FRI(Fast Reed-Solomon Interactive)プロトコルを適切に機能させるための鍵です。後者はアルゴリズムを非常に高速に実行します。各ラウンドのスケールは前のラウンドと比較して半分に削減されるため、合計計算コストはO(n)ではなくO(n)です。
ドメインの段階的な削減を実現するために、2対1のマッピングが使用されます。つまり、各ポイントが2つのポイントのいずれかにマッピングされます。このマッピングにより、データセットのサイズを半分に削減できます。この2対1のマッピングの重要な利点は、繰り返し可能であることです。つまり、このマッピングを適用すると、結果の結果セットが同じプロパティを保持します。乗法サブグループから始めてください。このサブグループは、各要素Xがセットに複数の2xを搭載しているセットSです。セットsで正方形操作を実行する場合(つまり、セットの各要素xをx^2にマップ)、新しいセットs^2は同じ属性を保持します。この操作により、データセットのサイズを削減し続けることができます。理論的には、データセットを残っている値が1つだけに絞り込むことができますが、実際には、より小さなセットに到達する前に停止します。
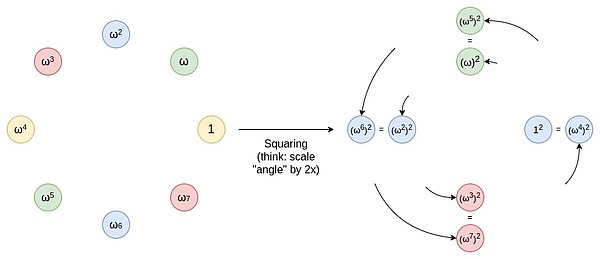
この操作は、円周上にライン(セグメントやアークなど)を延長するプロセスと考えることができ、周囲で2回転を回転させます。たとえば、ポイントが円周上のX度位置にある場合、この操作の後、2倍の位置に移動します。0〜179度の位置での円周上の各ポイントは、180〜359度の位置に対応するポイントがあり、これら2つのポイントが重複します。これは、Xから2倍のポイントをマッピングすると、X+180度の位置と一致することを意味します。このプロセスを繰り返すことができます。つまり、このマッピング操作を複数回適用できます。そのたびに、周囲に移動するたびに新しい位置に移動できます。
マッピング手法を効果的にするには、元の乗算サブグループのサイズを要因として2の大きなパワーを持たせる必要があります。babybearは、モジュラスが最大乗算サブグループにすべての非ゼロ値が含まれるような値である特定の弾性率を持つシステムであるため、サブグループのサイズは2k -1(kは弾性率のビット数)です。このサイズのサブグループは、マッピング操作を繰り返し適用することで多項式の程度を効果的に削減できるため、上記の手法に非常に適しています。BabyBearでは、サイズ2^kのサブグループを選択し(またはセット全体を直接使用)、FRIメソッドを適用して、多項式の程度を15に徐々に減らし、最後の多項式の程度を確認できます。この方法は、弾性率の特性と乗算サブグループのサイズを利用して、計算プロセスを非常に効率的にします。Mersenne31は、乗算サブグループのサイズが2^31-1になるように、何らかの値の弾性率を持つ別のシステムです。この場合、乗算サブグループの因子として2の電力は1つだけであるため、1回だけ分割するだけです。その後の処理は、上記の手法にも適用されなくなります。つまり、FFTを使用してbabybearのような効果的な多項式の程度削減を実行することは不可能です。
Mersenne31ドメインは、既存の32ビットCPU/GPU操作における算術操作に最適です。そのモジュラス特性(たとえば、2^{31} -1)のため、多くの操作は効率的なビット操作を使用して達成できます適切な範囲に減らします。変位操作は非常に効率的な操作です。乗算操作では、特定のCPU命令(通常は高ビット変位命令と呼ばれます)を使用して結果を処理できます。これらの命令は、乗算の高ビット部分を効率的に計算し、それにより操作の効率を改善することができます。Mersenne31ドメインでは、上記の特性により、算術操作はBabybearドメインの約1.3倍高速です。Mersenne31は、より高いコンピューティング効率を提供します。FRIをMersenne31ドメインに実装できる場合、これによりコンピューティング効率が大幅に向上し、FRIアプリケーションがより効率的になります。
サークル金
これは、プライムナンバーPを考えると、サークルスタークの賢さです。このグループは、特定の特定の条件を満たすすべてのポイントで構成されています。たとえば、x^2 mod pは特定の値のセットに等しくなります。
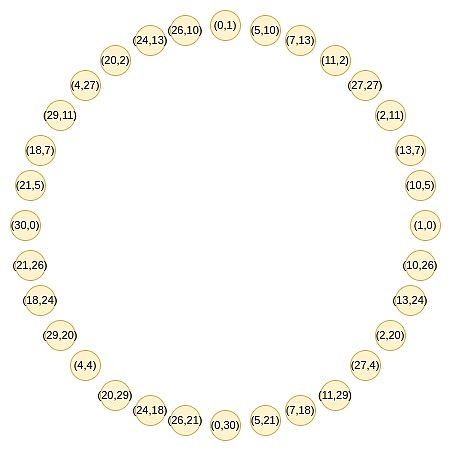
これらのポイントは、最近三角法または複雑な乗算を行った場合に慣れていると思われる追加の規則に従います。
(x_1、y_1) +(x_2、y_2)=(x_1x_2 -y_1y_2、x_1y_2 + x_2y_1)
二重の形式は次のとおりです。
2 *(x、y)=(2x^2-1、2xy)
それでは、この円の奇妙な位置のポイントに焦点を合わせましょう。
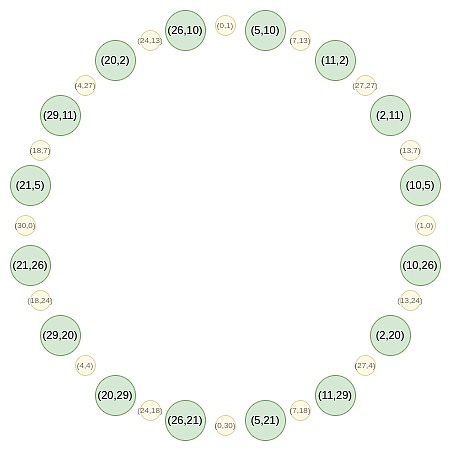
まず、すべてのポイントを直線に収束します。通常のFRIで使用するB(X²)およびC(X²)式の同等の形式は次のとおりです。
f_0(x)= \ frac {f(x、y) + f(x、-y)} {2}
次に、X-Lineのサブセットで定義されている1次元P(x)を取得するために、ランダムな線形結合を実行できます。
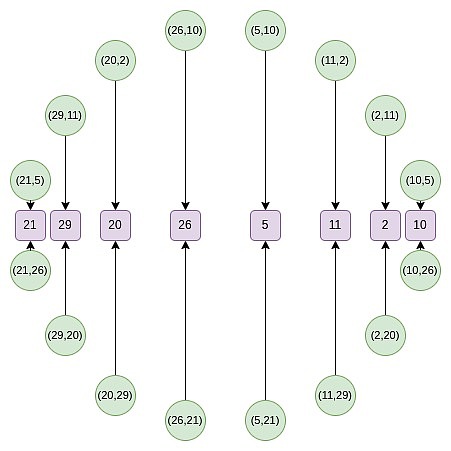
第2ラウンドから始めて、マッピングが変更されました。
f_0(2x^2-1)= \ frac {f(x) + f(-x)} {2}
このマッピングは、実際には上記のサイズを毎回半分に縮小します。ここで起こるのは、各xがある意味で2つのポイントを表すことです:(x、y)と(x、-y)。(x→2x^2-1)は、上記のポイント乗算ルールです。したがって、円の2つの反対ポイントのX座標を、乗算点のx座標に変換します。
たとえば、2番目の数値で円の右から数値の2番目の値を取得し、マッピング2→2(2^2)-1 = 7を適用すると、7の結果が得られます。元の円に戻ると、(2、11)は右から3番目のポイントであるため、乗算した後、右から6番目のポイント、つまり(7、13)を取得します。
これは2次元空間で行われた可能性がありますが、1次元空間で動作すると、プロセスがより効率的になります。
サークルFFT
FRIに密接に関連するアルゴリズムはFFTであり、多項式のn評価値を、多項式のn係数より低い程度で変換します。FFTのプロセスはFRIに似ていますが、各ステップでF_0とF_1のランダムな線形結合を生成する代わりに、FFTはそれらに半サイズのFFTを再帰的に実行し、FFT(F_0)の出力を均一な係数として取得します。奇数係数としてのFFT(F_1)の出力。
Circle GroupはFFTもサポートしています。FFTは、金と同様に構築されています。ただし、重要な違いは、サークルFFT(およびサークルFRI)によって処理されたオブジェクトが厳密に多項式ではないことです。代わりに、それらは数学的にRiemann -Rochスペースと呼ばれるものです。この場合、多項式はモジュール式丸である(x^2 + y^2-1 = 0)。つまり、x^2 + y^2-1の倍数をゼロとして扱います。それを理解する別の方法は次のとおりです。yの1つのパワーのみを許可します。y^2用語が表示されたら、1 -x^2に置き換えます。
これはまた、サークルFFTによる出力係数が通常のFRIのように一等式ではないことを意味します(たとえば、通常のFRI出力が[6、2、8、3]の場合、これはp(x)= 3x^を意味することがわかっています。 3 + 8x^2 + 2x + 6)。代わりに、円fftの係数は円fftの基礎です:{1、y、x、xy、2x^2-1、2x^2y -y、2x^3 -x、2x^3y -xy、8x^4 -8x^2 + 1 …}
良いニュースは、開発者として、これをほぼ完全に無視できるということです。スタークスは、係数を知る必要はありません。代わりに、多項式を特定のドメインに一連の評価値として保存するだけです。FFTを使用する唯一の場所は、(Riemann-Roch Spaceに類似した)低級拡張を実行することです。N値が与えられた場合、すべて同じ多項式でk*n値を生成します。この場合、FFTを使用して係数を生成し、これらの係数に(k-1)nゼロを追加してから、逆fftを使用して評価値のより大きなセットを取得できます。
Circle FFTだけが特別なFFTタイプではありません。楕円曲線FFTは、有限ドメイン(プライムドメイン、バイナリドメインなど)で動作できるため、より強力です。ただし、ECFFTはより複雑で非効率的であるため、P = 2^{31} -1でサークルFFTを使用できるため、使用することを選択しました。
ここから、私たちはいくつかのよりあいまいな詳細を深く説明し、サークルスタークの実装を実装する詳細は、通常のスタークのものとは異なります。
商
Starkプロトコルでは、一般的な操作は、特定のポイントで商操作を実行することです。これは、意図的またはランダムに選択できます。たとえば、p(x)= yを証明したい場合は、次のことを行うことができます。
コンピューティング商:多項式p(x)と定数y、計算指数q = {p -y}/{x -x}を計算すると、xは選択されたポイントです。
証明多項式:証明Qは多項式であり、分数値ではありません。このようにして、p(x)= yが真であることが証明されています。
さらに、Deep-FRIプロトコルでは、評価ポイントのランダムな選択は、Merkleブランチの数を減らし、それによりFRIプロトコルのセキュリティと効率を改善することです。
サークルグループのスタークプロトコルを扱う場合、単一のポイントに渡すことができる線形関数がないため、従来の商の動作方法を置き換えるために異なる手法を使用する必要があります。これには通常、サークルグループに固有の幾何学的特性を使用した新しいアルゴリズムの設計が必要です。
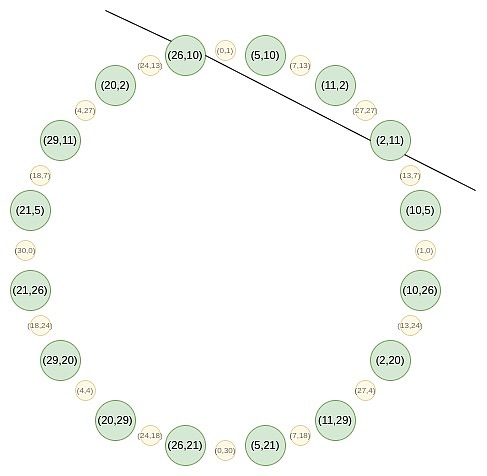
サークルグループでは、ポイント(P_X、P_Y)で接線に接線関数を構築できますが、この関数はポイントを介して2つの2つ、つまり、多項式を線形関数の倍数にするために、 、その時点でのみゼロであるよりも、より厳しい状態を満たす必要があります。したがって、ある時点で評価結果を証明することはできません。それで、私たちはそれにどのように対処すべきですか?
この課題を2つの点で評価することで証明され、焦点を合わせる必要がない仮想ポイントを追加することで証明しなければなりませんでした。

線関数: + + c。方程式に変換し、0に等しいように強制すると、高校の数学の標準形式と呼ばれるものの線として認識される場合があります。
多項式PがX_1でY_1とX_2でY_2に等しい場合、X_1でY_1、X_2でY_2に等しい補間関数Lを選択できます。これは、l = \ frac {y_2 -y_1} {x_2 -x_1} \ cdot(x -x_1) + y_1として単純に表現できます。
次に、l(p -lが両方のポイントでゼロになるように)とl(すなわち、x_2 -x_1の間の線形関数)をlで割ることにより、x_1のy_1およびx_2のy_2に等しいことを証明します。商Qが多項式であることを証明します。
消失多項式
スタークでは、あなたが証明しようとしている多項式方程式は通常、c(p(x)、p({next}(x)))= z(x)•(x)のように見えます。ここで、z(x)は多項式です元の評価ドメイン全体でゼロに等しくなります。通常のスタークでは、この関数はx^n -1です。円形のスタークでは、対応する関数は次のとおりです。
z_1(x、y)= y
Z_2(x、y)= x
z_ {n+1}(x、y)=(2 * z_n(x、y)^2)-1
崩壊関数から消滅する多項式を推測できることに注意してください。通常のスタークでは、x→x^2を再利用しますが、円形のスタークではx→2x^2-1を再利用します。ただし、最初のラウンドでは、最初のラウンドが特別なため、さまざまなトリートメントを行います。
リバースビットオーダー
スタークでは、多項式の評価は通常、「自然な」順序で配置されません(例:p(ω)、p(ω2)、…、p(ωn -1)が、逆逆ビット順序と呼ばれるものに基づいています:
p(\ omega^{\ frac {3n} {8}})
n = 16を設定し、評価するωのパワーのみに焦点を合わせると、リストは次のようになります。
{0、8、4、12、2、10、6、14、1、9、5、13、3、11、7、15}
この種の重要なプロパティには、FRI評価の初期にグループ化された価値が隣接する重要なプロパティがあります。たとえば、FRIグループXと-Xの最初のステップ。n = 16の場合、ω^8 = -1、これはp(ω^i))および(p(-ω^i)= p(ω^{i+8})\)を意味します。私たちが見ることができるように、これらはまさに隣同士の正しいペアです。FRIグループP(ω^I)、p(ω^{i+4})、p(ω^{i+8})、およびp(ω^{i+12})の2番目のステップ。これらはまさに4つのグループで見られるものです。これを行うと、FRIはさらに空間を節約できます。これにより、折り畳まれた値のマークルプルーフを提供できるためです(または、kホイールを一度に折りたたむと、すべての2^k値)。
サークルスタークでは、最初のステップでは(x、y)と(x、y)とペアリングされますq、p、q、q^i(p)= -q^i(q)を選択します。ここで、q^iはマッピングx→2x^2-1 iです。円の位置からこれらのポイントを考慮すると、各ステップで、これは最初のポイントと最後のポイント、2番目のポイントが最後から2番目のポイントなどを組み合わせたように見えます。
この折りたたみ構造を反映するように逆ビットの順序を調整するには、最後のビットを除く各ビットを反転する必要があります。最後のビットを保持し、それを使用して、他のビットをひっくり返すかどうかを決定します。
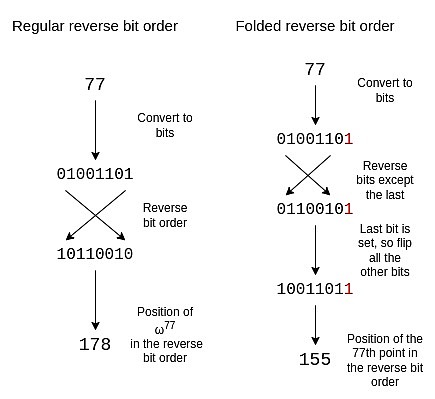
サイズ16の折り畳まれた逆ビット順序は次のとおりです。
{0、15、8、7、4、11、12、3、2、13、10、5、6、9、9、14、1}
前のセクションで円を観察すると、ポイント0、15、8、7(右から反時計回り)は(x、y)、(x、-y)、(-x、 – – y)および(-x、y)形式。これはまさに必要なものです。
効率
これらのプロトコルは、サークルスターク(および一般的に31ビットプライムスターク)で非常に効率的です。サークルスタークで証明された計算には、通常、いくつかのタイプの計算が含まれます。
1。ネイティブ算術:カウントなどのビジネスロジックに使用されます。
2。ネイティブ算術:Poseidonのようなハッシュ関数など、暗号化で使用されます。
3.パラメーターを見つける:表から値を読み取ることでさまざまな計算を実装する一般的かつ効率的な計算方法。
効率の重要な尺度は、コンピューティングトラッキングでは、有用な作業のためにスペース全体を最大限に活用するか、多くの空きスペースを残すことです。大きなフィールドのうなり声では、多くの場合、多くの自由空間があります。通常、ビジネスロジックとルックアップテーブルには少数の計算が含まれます(これらの数値はnよりも少ないことが多く、nは計算ステップの総数であり、したがって2^未満です。 {実際には25})、ただし、サイズ2^{256}のビットフィールドを使用するコストを支払う必要があります。ここで、フィールドのサイズは2^{31}なので、無駄なスペースはそれほど多くありません。スナーク(ポセイドンなど)のために設計された低算術の複雑さのハッシュは、あらゆるフィールドの追跡の各数値をすべてのビットを最大限に活用します。
ビニウスは、より効率的なビットパッキングのためにさまざまなサイズのフィールドを混ぜることができるため、サークルスタークよりも優れたソリューションです。ビニウスは、ルックアップテーブルのオーバーヘッドを増やすことなく、32ビットの追加を実行するオプションも提供します。ただし、これらの利点の価格(私の意見では)は、コンセプトがより複雑になるのに対し、サークルスターク(およびベビーベアに基づく通常のスターク)は概念的に比較的単純なものです。
結論:サークルスタークに関する私の意見
サークルは、スタークスほど開発者にとって複雑なものはありません。実装プロセス中、上記の3つの質問は基本的に従来の金との違いです。Circle Friが運営する多項式の背後にある数学は非常に複雑であり、それを理解し評価するのに時間がかかりますが、この複雑さは実際には顕著に隠されておらず、開発者はそれを直接感じません。
Circle FriとCircle FFTを理解することは、他の特別なFFTを理解する方法でもあります。最も注目すべきは、Biniusや以前のLibstarkが使用したFFTなどのバイナリドメインFFT、および楕円曲線FFT、これらのより複雑な構成要素です。より多くの多くのマッピングを使用したFFTは、楕円曲線ポイント操作と十分に組み合わせることができます。
Mersenne31、BabyBear、およびBiniusのようなバイナリドメインテクノロジーを組み合わせて、Starksの基本層の効率性に近づいていると感じています。この時点で、Starkの最適化方向には次の重要なポイントがあると思います。
ハッシュ関数と署名の効率を最大化するための算術:ハッシュ関数やデジタル署名などの基本的な暗号化プリミティブを最も効率的な形式に最適化し、厳しい証明で使用すると最適なパフォーマンスを実現できるようにします。これは、これらのプリミティブが計算努力を減らし、効率を向上させるための特別な最適化を意味します。
より並列化を可能にするために再帰的な構造を実行します。再帰的な構造とは、スタークプルーフプロセスの異なるレベルへの再帰的適用を指し、それにより並列処理能力が向上します。このようにして、コンピューティングリソースをより効率的に使用でき、証明プロセスを加速できます。
開発者エクスペリエンスを向上させる算術仮想マシン:仮想マシンの算術処理により、開発者がコンピューティングタスクを作成および実行できるようになります。これには、スタークコントラクトやその他のコンピューティングタスクを構築およびテストする際の開発者のエクスペリエンスを改善するための仮想マシンの最適化、開発者のエクスペリエンスが改善されます。








