
Título original: «Explorando Circle Starks» escrito por Vitalik Buterin, cofundador de Ethereum compilado por Chris, Techub News
La premisa de comprender este artículo es que ya ha entendido los principios básicos de los snarks y los Starks.Si no está familiarizado con esto, se recomienda que lea las primeras partes de este artículo para aprender lo básico.
En los últimos años, la tendencia del diseño del protocolo Starks es cambiar a usar campos más pequeños.Las primeras implementaciones de producción de Starks utilizaron campos de 256 bits, que fueron operaciones modulares en grandes cantidades (como 21888 … 95617), lo que hizo que estos protocolos sean compatibles con firmas basadas en curvas elípticas.Sin embargo, este diseño es relativamente ineficiente. Solo se requiere una novena del tiempo de cálculo.Para resolver este problema, Starks comenzó a recurrir a campos más pequeños: los primeros Ricitos de oro, luego Mersenne31 y Babybear.
Este cambio mejora la velocidad de prueba, como la capacidad de Starkware para probar 620,000 hashes Poseidon2 por segundo en una computadora portátil M3.Esto significa que mientras estemos dispuestos a confiar en Poseidon2 como una función hash, podemos resolver el problema en el desarrollo de ZK-EVM eficiente.Entonces, ¿cómo funcionan estas tecnologías?¿Cómo se establecen estas pruebas en campos más pequeños?¿Cómo se comparan estos protocolos con soluciones como Binius?Este artículo explorará estos detalles, centrándose específicamente en un esquema llamado Circle Starks (stwo en Starkware, Plonky3 en Polygon y mi propia versión implementada en Python), que tiene propiedades únicas que son compatibles con el campo Mersenne31.
Problemas comunes al usar campos de matemáticas más pequeñas
Al crear pruebas basadas en hash (o cualquier tipo de prueba), una técnica muy importante es verificar indirectamente las propiedades de los polinomios al probar los resultados de la evaluación de polinomios en puntos aleatorios.Este enfoque puede simplificar enormemente el proceso de prueba, ya que la evaluación en puntos aleatorios suele ser mucho más fácil que tratar con todo el polinomio.
Por ejemplo, suponga que un sistema de prueba requiere que genere un compromiso para los polinomios, a, debe satisfacer a^3 (x) + x – a (\ omega*x) = x^n (uno muy común en el zk -snark Tipo de prueba de protocolo).¿El protocolo puede pedirle que seleccione una coordenada aleatoria?Luego invertir a (r) = c, demuestra que q = \ frac {a – c} {x – r} es un polinomio.
Si comprende los detalles del protocolo o los mecanismos internos de antemano, puede encontrar formas de omitir o descifrar estos protocolos.Se pueden mencionar operaciones o métodos específicos a continuación para lograr esto.Por ejemplo, para satisfacer la ecuación A (\ omega * r), puede establecer un (r) a 0 y luego hacer una línea recta que pasa a través de estos dos puntos.
Para evitar estos ataques, necesitamos seleccionar R después de que el atacante proporcione un (Fiat-Shamir es una tecnología utilizada para mejorar la seguridad del protocolo, evitando los ataques estableciendo ciertos parámetros en un cierto valor hash. Los parámetros deben provenir de un conjunto lo suficientemente grande. Para garantizar que el atacante no pueda predecir o adivinar estos parámetros, mejorando así la seguridad del sistema.
En el protocolo y los Starks basados en la curva elíptica en el período de 2019, este problema es simple: todas nuestras matemáticas se realizan en números de 256 bits, por lo que podemos seleccionar R como un número aleatorio de 256 bits para que podamos hacerlo ahora.Sin embargo, en Starks en campos más pequeños, tenemos un problema: solo hay alrededor de 2 mil millones de valores R posibles para elegir, por lo que un atacante que quiere falsificar pruebas solo necesita probar 2 mil millones de veces, aunque la carga de trabajo es alta, Pero para un atacante que está decidido, ¡todavía se puede hacer!
Hay dos soluciones a este problema:
-
Realizar múltiples controles aleatorios
-
Campos extendidos
La forma más simple y efectiva de realizar múltiples controles aleatorios: en lugar de verificar una coordenada, es mejor verificar cuatro coordenadas aleatorias repetidamente.Esto es teóricamente factible, pero hay problemas de eficiencia.Si está tratando con un polinomio con un grado menor que cierto valor y operando en un dominio de cierto tamaño, un atacante puede construir un polinomio malicioso que se vea normal en estas posiciones.Por lo tanto, si pueden romper con éxito el protocolo es una pregunta probabilística, por lo que el número de rondas de controles debe aumentar para mejorar la seguridad general y garantizar una defensa efectiva contra los atacantes.
这引出了另一个解决方案:扩展域,扩展域类似于复数,但它是基于有限域的。Introducimos un nuevo valor, denotado como α \ alphaα, y declaramos que satisface una determinada relación, como α2 = algún valor \ alpha^2 = \ text {algún valor} α2 = algún valor.De esta manera, creamos una nueva estructura matemática que permite operaciones más complejas en dominios finitos.En este dominio extendido, el cálculo de la multiplicación se convierte en una multiplicación utilizando el nuevo valor α \ alfaα.Ahora podemos manipular pares de valor en dominios extendidos, no solo números individuales.Por ejemplo, si trabajamos en campos como Mersenne o Babybear, dicha extensión nos permite tener más opciones de valor, mejorando así la seguridad.Para aumentar aún más el tamaño del campo, podemos aplicar repetidamente la misma técnica.Dado que hemos usado α \ alphaα, necesitamos definir un nuevo valor, que en Mersenne31 se manifiesta como seleccionando α \ alphaα de modo que α2 = algún valor \ alpha^2 = \ text {algún valor} α2 = algún valor.

Código (puede mejorarlo con Karatsuba)
Al extender el dominio, ahora tenemos suficientes valores para elegir satisfacer nuestras necesidades de seguridad.Si se trata de un polinomio con un grado más pequeño que DDD, cada ronda puede proporcionar seguridad de 104 bits.Esto significa que tenemos suficiente seguridad.Si necesita alcanzar un nivel de seguridad más alto, como 128 bits, podemos agregar un trabajo informático adicional al protocolo para mejorar la seguridad.
Los dominios extendidos solo se usan en el protocolo de FRI (interactivo de solomón de láminas rápidas) y otros escenarios que requieren combinaciones lineales aleatorias.La mayoría de las operaciones matemáticas todavía se realizan en campos básicos, que generalmente son campos que son Modulo PPP o QQQ.Mientras tanto, casi todos los datos hash se realizan en el campo base, por lo que cada valor solo tiene cuatro bytes hash.Hacerlo puede aprovechar la eficiencia de los campos pequeños, mientras se utiliza campos más grandes cuando se requieren mejoras de seguridad.
Viernes regulares
Al construir Snark o Stark, el primer paso suele ser la aritmetización.Esto es para traducir problemas computacionales arbitrarios en una ecuación donde algunas variables y coeficientes son polinomios.Específicamente, esta ecuación generalmente se verá como p (x, y, z) = 0p (x, y, z) = 0, donde p es un polinomio, x, y y z es el parámetro dado, y el solucionador necesita Proporcione los valores de X e Y.Una vez que tal ecuación está presente, la solución de la ecuación corresponde a la solución del problema computacional subyacente.
Para demostrar que tiene una solución, debe demostrar que el valor que propone es de hecho un polinomio razonable (en lugar de una fracción, o en algunos lugares parece un polinomio y en otros lugares es un polinomio diferente, etc.) Y estos polinomios tienen un cierto grado máximo.Para hacer esto, utilizamos una técnica de combinación lineal aleatoria paso a paso:
-
Supongamos que tiene un valor de evaluación del polinomio a, y desea demostrar que su grado es inferior a 2^{20}
-
Considere el polinomio b (x^2) = a (x) + a (-x), c (x^2) = \ frac {a (x)-a (-x)} {x}
-
D es una combinación lineal aleatoria de B y C, es decir, D = B+RCD = B+RCD = B+RC, donde R es un coeficiente aleatorio.
Esencialmente, ¿lo que sucede es B aislamientos incluso coeficientes A, y?Dado B y C, puede restaurar el polinomio original A: A (x) = B (x^2) + xc (x^2).Si el grado de A es de hecho menor que 2^{20}, entonces los grados de B y C serán los grados de A y los grados de A, respectivamente, menos 1.Porque la combinación de términos pares y impares no aumenta el grado.Dado que D es una combinación lineal aleatoria de B y C, el grado de D también debe ser el grado de A, lo que le permite verificar si el grado de A cumple con los requisitos por el grado de D.
Primero, FRI simplifica el proceso de verificación al simplificar el problema de probar el grado polinomial de D al problema de probar el grado polinomial de D/2.Este proceso se puede repetir varias veces, simplificando el problema a mitad de camino cada vez.
El principio de funcionamiento del viernes es repetir este proceso simplificado.Por ejemplo, si comienza con una prueba de que el polinomio es D, a través de una serie de pasos, eventualmente se prueba que el polinomio es d/2.Después de cada simplificación, el grado del polinomio generado se reduce gradualmente.Si la salida de una etapa no es el grado polinomial esperado, esta ronda de comprobaciones fallará.Si alguien intenta empujar un polinomio que no es un grado D a través de esta técnica, entonces en la segunda ronda de producción, el grado tendrá una cierta probabilidad de que no cumpla con las expectativas, y en la tercera ronda, habrá más probable ser una situación de no conformidad.Este diseño puede detectar y rechazar efectivamente las entradas que no cumplan con los requisitos.Si el conjunto de datos es igual a un polinomio con un grado D en la mayoría de los lugares, este conjunto de datos tiene el potencial de ser validado por el viernes.Sin embargo, para construir dicho conjunto de datos, un atacante necesita conocer el polinomio real, por lo que incluso una ligera prueba defectuosa indica que el Prover puede generar una prueba «real».
Echemos un vistazo más de cerca a lo que está sucediendo aquí y las propiedades necesarias para que esto funcione.En cada paso, reducimos el número de polinomios a la mitad, al tiempo que reducimos el conjunto de puntos (el conjunto de puntos en los que nos enfocamos) a la mitad.El primero es la clave para hacer que el protocolo FRI (Rast Reed-Solomon Interactive) funcione correctamente.Este último hace que el algoritmo funcione extremadamente rápido: dado que la escala de cada ronda se reduce a la mitad en comparación con la ronda anterior, el costo total de cálculo es o (n), no o (n*log (n)).
Para lograr una reducción gradual en el dominio, se usa un mapeo de dos a uno, es decir, cada punto se asigna a uno de los dos puntos.Este mapeo nos permite reducir el tamaño de nuestro conjunto de datos por la mitad.Una ventaja importante de este mapeo dos a uno es que es repetible.Es decir, cuando aplicamos este mapeo, el conjunto de resultados resultante aún conserva las mismas propiedades.Supongamos que comenzamos con un subgrupo multiplicativo.Este subgrupo es un conjunto S donde cada elemento X también tiene su múltiplo 2x en el conjunto.Si realiza una operación cuadrada en el conjunto s (es decir, mapea cada elemento x en el conjunto en x^2), el nuevo conjunto S^2 conserva los mismos atributos.Esta operación nos permite continuar reduciendo el tamaño del conjunto de datos hasta que terminemos con solo un valor restante.Aunque en teoría podemos reducir el conjunto de datos a un solo valor restante, en la práctica, generalmente se detendrá antes de alcanzar un conjunto más pequeño.
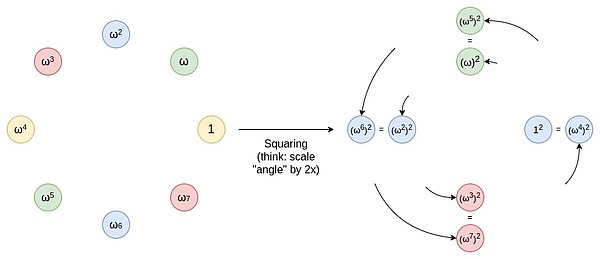
Puede pensar en esta operación como un proceso de extender una línea (por ejemplo, un segmento o un arco) en la circunferencia, lo que hace que gire dos vueltas alrededor de la circunferencia.Por ejemplo, si un punto está en una posición de grado x en la circunferencia, luego, después de esta operación, se mueve a una posición de 2x grado.Cada punto en la circunferencia en una posición de 0 a 179 grados tiene un punto correspondiente en una posición de 180 a 359 grados, y estos dos puntos se superpondrán.Esto significa que cuando asigna un punto de x a 2x grados, coincide con una posición a x+180 grados.Este proceso puede repetirse.Es decir, puede aplicar esta operación de mapeo varias veces, cada vez que se mueven los puntos en la circunferencia a su nueva posición.
Para que la técnica de mapeo sea efectiva, el tamaño del subgrupo de multiplicación original debe tener una gran potencia de 2 como factor.BabyBear es un sistema con un módulo específico cuyo módulo es un valor tal que su subgrupo de multiplicación máxima contiene todos los valores distantes de cero, por lo que el tamaño del subgrupo es 2K – 1 (donde K es el número de bits del módulo).Este subgrupo de tamaño es muy adecuado para la técnica anterior porque permite que el grado del polinomio se reduzca efectivamente aplicando repetidamente las operaciones de mapeo.En Babybear, puede seleccionar un subgrupo de tamaño 2^k (o usar directamente todo el conjunto), luego aplicar el método de FRI para reducir gradualmente el grado de polinomio a 15 y verificar el grado de polinomio al final.Este método utiliza las propiedades del módulo y el tamaño de los subgrupos de multiplicación, lo que hace que el proceso de cálculo sea muy eficiente.Mersenne31 es otro sistema con un módulo de algún valor, de modo que el tamaño del subgrupo de multiplicación es 2^31 – 1.En este caso, el subgrupo de multiplicación tiene solo un poder de 2 como factor, lo que solo lo hace dividir por 2 una vez.El procesamiento posterior ya no se aplica a las técnicas anteriores, es decir, es imposible usar FFT para realizar una reducción efectiva de grado polinómico como BabyBear.
El dominio Mersenne31 es ideal para operaciones aritméticas en operaciones CPU/GPU de 32 bits existentes.Debido a sus características del módulo (por ejemplo, 2^{31} – 1), se pueden lograr muchas operaciones utilizando operaciones de bits eficientes: si el resultado de agregar dos números excede el módulo, puede cambiar el resultado del módulo a la operación. reducir al rango apropiado.La operación de desplazamiento es una operación muy eficiente.En las operaciones de multiplicación, se pueden usar instrucciones específicas de CPU (generalmente llamadas instrucciones de desplazamiento de alto bits) para procesar los resultados.Estas instrucciones pueden calcular eficientemente la porción de alta bit de la multiplicación, mejorando así la eficiencia de la operación.En el dominio Mersenne31, debido a las características anteriores, las operaciones aritméticas son aproximadamente 1.3 veces más rápidas que en el dominio Babybear.Mersenne31 proporciona una mayor eficiencia informática.Si se puede implementar FRI en el dominio Mersenne31, esto mejorará significativamente la eficiencia informática y hará que las aplicaciones de FRI sean más eficientes.
FRI Círculo
Esta es la inteligencia de Circle Starks.Este grupo está compuesto por todos los puntos que cumplen con ciertas condiciones específicas, por ejemplo, X^2 Mod P es igual a un conjunto de puntos donde un valor específico.
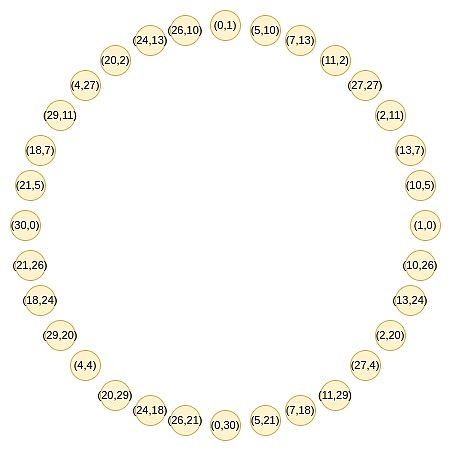
Estos puntos siguen una regla de suma, con la que puede encontrar familiarizado si ha realizado trigonometría o multiplicación compleja recientemente.
(x_1, y_1) + (x_2, y_2) = (x_1x_2 – y_1y_2, x_1y_2 + x_2y_1)
La forma doble es:
2 * (x, y) = (2x^2 – 1, 2xy)
Ahora, centrémonos en los puntos en la posición impar en este círculo:
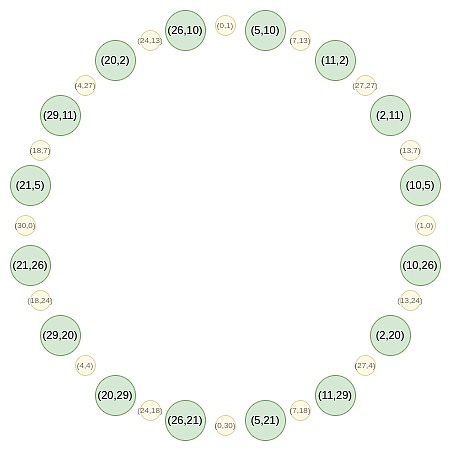
Primero, convergimos todos los puntos en una línea recta.Las formas equivalentes de las fórmulas B (x²) y C (x²) que usamos en FRI regular son:
f_0 (x) = \ frac {f (x, y) + f (x, -y)} {2}
Luego, podemos hacer combinaciones lineales aleatorias para obtener una P (x) unidimensional, que se define en un subconjunto de la línea X:
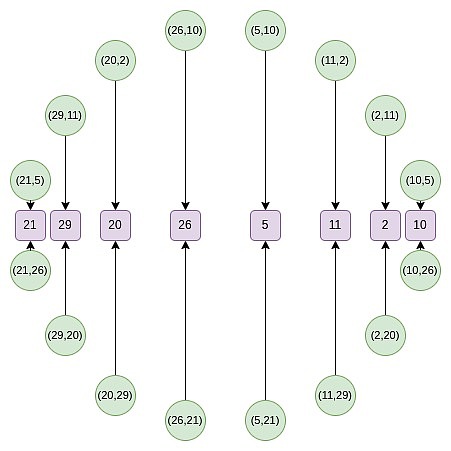
A partir de la segunda ronda, el mapeo cambió:
f_0 (2x^2-1) = \ frac {f (x) + f (-x)} {2}
Este mapeo en realidad reduce el tamaño del establecido anterior a la mitad cada vez, y lo que sucede aquí es que cada X representa dos puntos en un sentido: (x, y) y (x, -y).Y (x → 2x^2 – 1) es la regla de multiplicación de punto anterior.Por lo tanto, convertimos las coordenadas X de dos puntos opuestos en el círculo en las coordenadas X de los puntos multiplicados.
Por ejemplo, si tomamos el segundo valor del número desde la derecha del círculo en el segundo número y aplicamos el mapeo 2 → 2 (2^2) – 1 = 7, obtenemos un resultado de 7.Si volvemos al círculo original, (2, 11) es el tercer punto de la derecha, por lo que después de multiplicarlo, obtenemos el sexto punto de la derecha, es decir, (7, 13).
Esto podría haberse hecho en un espacio bidimensional, pero operar en un espacio unidimensional haría que el proceso sea más eficiente.
Circle FFTS
Un algoritmo estrechamente relacionado con FRI es FFT, que convierte los valores de evaluación de un polinomio con un grado inferior a los coeficientes de N a N del polinomio.El proceso de FFT es similar al FRI, excepto que en lugar de generar combinaciones lineales aleatorias de F_0 y F_1 en cada paso, FFT realiza recursivamente FFT de tamaño medio y toma la salida de FFT (F_0) como un coeficiente uniforme, toma el Salida de FFT (F_1) como un coeficiente impar.
Circle Group también es compatible con FFT, que se construye de manera similar a FRI.Sin embargo, una diferencia clave es que los objetos procesados por Circle FFT (y Circle Fri) no son estrictamente polinomiales.En cambio, son lo que se llama matemáticamente el espacio riemann -roch: en este caso, el polinomio está modularmente con círculo (x^2 + y^2 – 1 = 0).Es decir, tratamos cualquier múltiplo de x^2 + y^2 – 1 como cero.Otra forma de entenderlo es: solo permitimos una potencia de y: una vez que aparece el término y^2, lo reemplazamos con 1 – x^2.
Esto también significa que los coeficientes de salida del círculo FFT no son monomiales como un viernes regular (por ejemplo, si la salida de viernes regular es [6, 2, 8, 3], entonces sabemos que esto significa p (x) = 3x^^ 3 + 8x^2 + 2x + 6).En cambio, los coeficientes del círculo FFT son la base para el círculo FFT: {1, y, x, xy, 2x^2 – 1, 2x^2y – y, 2x^3 – x, 2x^3y – xy, 8x^4 – 8x^2 + 1 …}
La buena noticia es que, como desarrollador, puede ignorarlo casi por completo.Starks nunca requiere que conozca los coeficientes.En cambio, simplemente almacene el polinomio como un conjunto de valores de evaluación en un dominio específico.El único lugar para usar FFT es realizar (similar al espacio Riemann-Roch) expansión de bajo grado: dados los valores n, generar valores k*n, todos en el mismo polinomio.En este caso, puede usar FFT para generar coeficientes, agregar (k-1) n ceros a estos coeficientes, y luego usar el FFT inverso para obtener un conjunto más grande de valores de evaluación.
Circle FFT no es el único tipo FFT especial.Las FFT de la curva elíptica son más poderosas porque pueden trabajar en cualquier dominio finito (dominio principal, dominio binario, etc.).Sin embargo, ECFFT es más complejo e ineficiente, por lo que dado que podemos usar círculo FFT en p = 2^{31} -1, elegimos usarlo.
Desde aquí, profundizamos en algunos detalles más oscuros, y los detalles de la implementación de la implementación de Circle Starks son diferentes de los de los Starks regulares.
Cociente
En el protocolo Stark, una operación común es realizar operaciones de cociente en puntos específicos, que se pueden seleccionar intencionalmente o al azar.Por ejemplo, si desea demostrar que P (x) = y, puede hacerlo por:
Cociente de computación: Dado el polinomio p (x) y la constante y, el cociente de computación q = {p – y}/{x – x}, donde x es el punto seleccionado.
Polinomio de prueba: la prueba Q es un polinomio, no un valor fraccional.De esta manera, se demuestra que p (x) = y es verdadero.
Además, en el protocolo de vía fría, la selección aleatoria de los puntos de evaluación es reducir el número de ramas de Merkle, mejorando así la seguridad y la eficiencia del protocolo FRI.
Al tratar con el protocolo Stark del grupo Circle, dado que no hay una función lineal que se pueda pasar a través de un solo punto, se deben utilizar diferentes técnicas para reemplazar el método de operación del cociente tradicional.Esto generalmente requiere el diseño de nuevos algoritmos utilizando las propiedades geométricas exclusivas del grupo Circle.
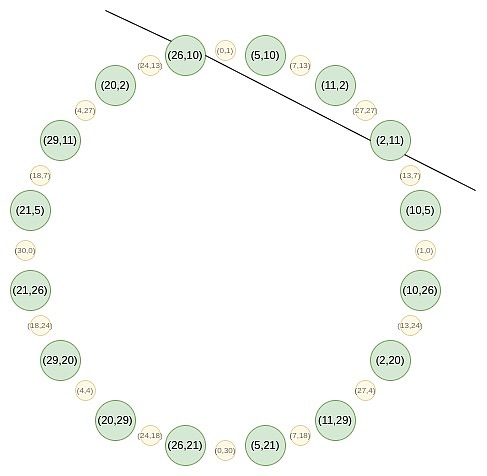
En el grupo círculo, puede construir una función tangente para tangente en un punto (p_x, p_y), pero esta función tendrá un gran número de 2 a través del punto, es decir, para hacer un polinomial el múltiplo de una función lineal , que debe satisfacer una condición más estricta que ser cero solo en ese punto.Por lo tanto, no puede probar los resultados de la evaluación en un punto.Entonces, ¿cómo debemos lidiar con eso?
Tuvimos que tomar este desafío, probado evaluándolo en dos puntos, agregando así un punto virtual en el que no necesitamos centrarnos.

Función de línea: ax + por + c.Si lo convierte en una ecuación y la obliga a igual a 0, entonces puede reconocerlo como una línea en lo que se llama una forma estándar en las matemáticas de la escuela secundaria.
Si tenemos una P polinomial es igual a Y_1 en X_1 e Y_2 en X_2, podemos elegir una función de interpolación L, que es igual a Y_1 en X_1 e Y_2 en X_2.Esto se puede expresar simplemente como l = \ frac {y_2 – y_1} {x_2 – x_1} \ cdot (x – x_1) + y_1.
Luego demostramos que P es igual a y_1 en x_1 e y_2 en x_2, restando L (de modo que p – L es cero en ambos puntos), y por L (es decir, una función lineal entre x_2 – x_1) dividida por L a L a L a L a L a L Demuestre que el cociente q es un polinomio.
Polinomios de desaparición
En marcado, la ecuación polinomial que está tratando de probar que generalmente se parece a C (P (x), P ({Next} (x))) = Z (x) ⋅ H (x), donde z (x) es un polinomio igual a cero en todo el dominio de evaluación original.En Stark regular, esta función es x^n – 1.En una clara circular, la función correspondiente es:
Z_1 (x, y) = y
Z_2 (x, y) = x
Z_ {n+1} (x, y) = (2 * z_n (x, y)^2) – 1
Tenga en cuenta que puede deducir el polinomio de desaparición de la función de colapso: en un Stark regular, reutiliza x → x^2, mientras que en una clara circular reutiliza x → 2x^2 – 1.Sin embargo, para la primera ronda, harás diferentes tratamientos porque la primera ronda es especial.
Orden de bits inverso
En Starks, la evaluación de los polinomios generalmente no se organiza en orden «natural» (por ejemplo, P (Ω), P (ω2), …, P (ωn – 1), pero se basa en lo que yo llamo el orden inverso de bits inversa :
P (\ Omega^{\ frac {3n} {8}})
Si establecemos n = 16 y nos enfocamos solo en qué poderes de Ω evaluamos, la lista se ve así:
{0, 8, 4, 12, 2, 10, 6, 14, 1, 9, 5, 13, 3, 11, 7, 15}
Este tipo tiene una propiedad clave que los valores agrupados al principio de la evaluación de FRI serán adyacentes en el tipo.Por ejemplo, el primer paso de los grupos de viernes x y -x.En el caso de n = 16, ω^8 = -1, que significa p (ω^i)) y (p (-ω^i) = p (ω^{i+8}) \).Como podemos ver, estos son exactamente los pares correctos uno al lado del otro.El segundo paso de los grupos de fri p (ω^i), p (ω^{i+4}), p (ω^{i+8}) y p (Ω^{i+12}).Esto es exactamente lo que vemos en cuatro grupos, y así sucesivamente.Hacer esto hace que el viernes sea aún más ahorro de espacio porque le permite proporcionar una prueba de merkle para los valores que se doblan (o, si dobla las ruedas k a la vez, todos los valores de 2^k).
En Circle Starks, la estructura de pliegue es ligeramente diferente: en el primer paso emparejamos (x, y) con (x, -y); Q, seleccione P y Q de modo que Q^i (P) = -q^i (Q), donde Q^I es un mapeo repetido x → 2x^2-1 i veces.Si consideramos estos puntos desde la posición en el círculo, entonces en cada paso, este parece el primer punto emparejado con el último punto, el segundo punto combinado con el penúltimo punto, y así sucesivamente.
Para ajustar el orden de bits inverso para reflejar esta estructura plegable, necesitamos invertir cada bit, excepto el último bit.Mantenemos el último bit y lo usamos para decidir si voltea los otros bits.
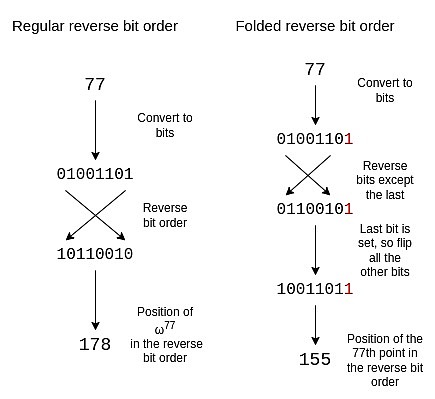
Un orden de bits inverso plegado del tamaño 16 es el siguiente:
{0, 15, 8, 7, 4, 11, 12, 3, 2, 13, 10, 5, 6, 9, 14, 1}
Si observa el círculo en la sección anterior, encontrará que los puntos 0, 15, 8 y 7 (en sentido antihorario de la derecha) son (x, y), (x, -y), (-x, – – – – y) y (-x, y) formas, que son exactamente lo que necesitamos.
eficiencia
Estos protocolos son muy eficientes en Starks circulares (y generalmente Starks principales de 31 bits).Un cálculo probado en Circle Stark generalmente involucra varios tipos de cálculos:
1. Aritmética nativa: utilizado para la lógica de negocios, como contar.
2. Aritmética nativa: utilizado en criptografía, como funciones hash como Poseidón.
3. Encuentre parámetros: un método de cálculo general y eficiente que implementa varios cálculos leyendo valores de las tablas.
La medida clave de la eficiencia es: en el seguimiento de la computación, ¿aprovecha al máximo todo el espacio para un trabajo útil o deja mucho espacio libre?En los snarks en campos grandes, a menudo hay mucho espacio libre: la lógica comercial y las tablas de búsqueda generalmente implican cálculos de pequeños números (esos números a menudo son menores que n, n es el número total de pasos de cálculo y, por lo tanto, menos de 2^ {25 en la práctica}), pero aún debe pagar el costo de usar un campo de bit de tamaño 2^{256}.Aquí, el tamaño del campo es 2^{31}, por lo que el espacio desperdiciado no es mucho.Los hashes de baja complejidad aritmética diseñados para sarcases (como Poseidón) aprovechan al máximo cada bit de cada número en el seguimiento en cualquier campo.
Binius es una mejor solución que Circle Starks porque le permite mezclar campos de diferentes tamaños para un embalaje de bits más eficiente.Binius también proporciona la opción de realizar una adición de 32 bits sin aumentar la sobrecarga de la tabla de búsqueda.Sin embargo, el precio de estas ventajas (en mi opinión) es que harán que el concepto sea más complejo, mientras que los Starks círculo (y los Starks regulares basados en Babybear) son relativamente simples conceptualmente.
Conclusión: Mi opinión sobre Circle Starks
Circle Stark no es más complicado para los desarrolladores que Starks.Durante el proceso de implementación, las tres preguntas mencionadas anteriormente son básicamente la diferencia con el VIA convencional.Aunque las matemáticas detrás de los polinomios operados por Circle Fri son muy complejos y lleva algún tiempo comprenderlo y apreciarlo, esta complejidad en realidad está oculta de manera menos visible y los desarrolladores no lo sentirán directamente.
Comprender el círculo de fts y círculo también puede ser una forma de comprender otros FFT especiales: los más notables son las FFT de dominio binario, como las FFT utilizadas por Binius y el Libstark anterior, y algunas construcciones más complejas, como FFTS de curva elíptica, estos, estas Las FFT que usan un mapeo menos a muchos pueden combinarse bien con la operación del punto de curva elíptica.
Combinando las tecnologías de Mersenne31, Babybear y Binary Domain como Binius, sentimos que nos estamos acercando a los límites de eficiencia de la capa base de Starks.En este punto, espero que la dirección de optimización de Stark tenga los siguientes puntos clave:
Aritmética para maximizar la eficiencia de las funciones y firmas del hash: optimizar las primitivas criptográficas básicas como las funciones hash y las firmas digitales en la forma más eficiente, para que puedan lograr un rendimiento óptimo cuando se usan en pruebas marcadas.Esto significa optimizaciones especiales para estas primitivas para reducir el esfuerzo computacional y aumentar la eficiencia.
Realice una construcción recursiva para permitir una mayor paralelización: la construcción recursiva se refiere a la aplicación recursiva del proceso de prueba de Stark a diferentes niveles, mejorando así la potencia de procesamiento paralelo.De esta manera, los recursos informáticos se pueden usar de manera más eficiente y el proceso de prueba se puede acelerar.
Máquinas virtuales aritméticas para mejorar la experiencia del desarrollador: el procesamiento aritmético de máquinas virtuales hace que sea más eficiente y simple para los desarrolladores crear y ejecutar tareas de computación.Esto incluye optimizar las máquinas virtuales para facilitar el uso en pruebas más marcadas, mejorar la experiencia de los desarrolladores al construir y probar contratos inteligentes u otras tareas informáticas.








