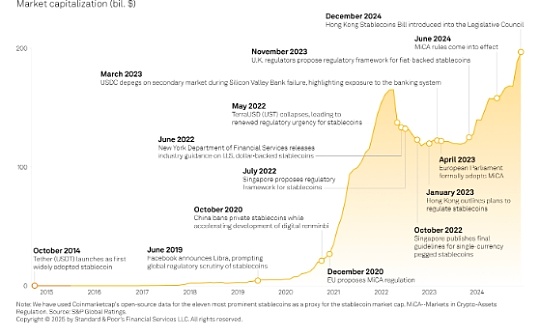
Source: Denglian Community
Zero-knowledge, concise, non-interactive proof of knowledge (zk-SNARKs) are powerful cryptographic primitives that allow one party, i.e., the proof, to convince the other party, that a statement is true without revealing it.Any other information other than the validity of this statement.They have attracted widespread attention due to their applications in verifiable private computing, providing proof of the correctness of computer program execution, and helping to scale blockchains.We believe that SNARKs will have a significant impact on shaping our world, as we have in our article[6]as described in.SNARKs are a general term for different types of proof systems, using different polynomial commitment schemes (PCS), arithmetic schemes, interactive Oracle proofs (IOP), or probabilistic checkable proofs (PCP).However, these basic ideas and concepts date back to the mid-1980s.Development efforts have accelerated significantly after the introduction of Bitcoin and Ethereum, which proves that they are an exciting and powerful use case because you can use zero-knowledge proofs (often called the proof of validity of this particular use case)Expand them.SNARKs are an important tool for blockchain scalability.As Ben-Sasson describes, the past few years have witnessed the Cambrian outbreak of crypto-proof[7].Each proof system has its advantages and disadvantages, and certain trade-offs are taken into account when designing.Advances in hardware, better algorithms, new arguments and gadgets have led to performance improvements and the birth of new systems.Many of these systems are being used in production and we keep pushing the boundaries.Will we have a universal proof system for all applications, or several systems for different needs?We think that there is little chance that a proof system will dominate all applications because:
-
Diversity of applications.
-
We have different constraint types (about memory, verification time, proof time).
-
The need for robustness (if a proof system is cracked, we still have other systems).
Even if the proof system changes greatly, they all have an important feature: proofs can be verified quickly.Difficulties associated with changing the underlying layer (such as Ethereum) are also solved by having proof-of-verification proof-of-working layers and easily adapted to the layers that handle new proof-of-work systems.
To outline the different characteristics of SNARKs:
-
Password hypothesis: anti-collision hash function, discrete logarithmic problems on elliptic curves, exponential knowledge.
-
Transparent vs Trusted Settings.
-
Proofreader time: linear vs hyperlinear.
-
Verifier time: constant time, logarithmic, sublinear, linear.
-
Proof size.
-
The convenience of recursion.
-
Arithmetic scheme.
-
unary vs multivariate polynomial.
This article will explore the origins of SNARKs, some basic building blocks, and the rise (and decline) of different proof systems.This article does not intend to conduct a detailed analysis of the proof system.Instead, we focus on those that have an impact on us at the moment.Of course, these developments can only be achieved based on the great work and ideas of the pioneers in this field.
Basic knowledge
As we mentioned, zero-knowledge proof is not new.Definitions, foundations, important theorems and even important protocols were established in the mid-1980s.Some of the key ideas and protocols used to build modern SNARKs were proposed in the 1990s (sumcheck protocol), even before Bitcoin emerged (GKR in 2007).The main problems adopted at that time were mainly related to the lack of strong use cases (the Internet was not as developed as it is in the 1990s) and the required computing power.
Zero Knowledge Proof: Origin (1985/1989)
The field of zero-knowledge proof first appeared in academic literature at [Goldwasser, Micali and Rackoff](https://people.csail.mit.edu/silvio/Selected Scientific Papers/Proof Systems/The_Knowledge_Complexity_Of_Interactive_Proof_Systems.pdf?ref=blog.lambdaclass.com “Goldwasser, Micali and Rackoff”) paper.For a discussion of origin, you can refer to the following video[8].This paper introduces the concepts of completeness, correctness and zero knowledge, and provides the construction of quadratic residuosity and quadratic non-residuosity.
Sumcheck Agreement (1992)
sumcheck protocol[9]Is by Lund, Fortnow, Karloff, and Nisan[10]Proposed in 1992.It is one of the most important building blocks for proof of concise interaction.It helps us reduce the declaration of sum of evaluations of multiple polynomials to a single evaluation on randomly selected points.
Goldwasser-Kalai-Rothblum (GKR) (2007)
GKR Protocol[11]It is an interactive protocol, where the running time of the prover is linearly related to the number of gates of the circuit, while the running time of the verifier is linearly related to the size of the circuit.In this protocol, the prover and the verifier agree on an arithmetic circuit of fan-in-two on a finite domain of depth d, where layer d corresponds to the input layer and layer 0 corresponds toOutput layer.The protocol starts with a declaration of the circuit output and reduces it to a declaration of the previous layer value.By recursion, we can convert it into a declaration of the circuit input, which can be easily checked.These reductions are achieved through the sumcheck protocol.
KZG Polynomial Commitment Solution (2010)
KZG polynomial commitment scheme (PCS) Kate, Zaverucha, and Goldberg[12]A polynomial commitment scheme using bilinear pairing groups was introduced in 2010.This commitment consists of a single group element and the committer can effectively open the commitment to any correct evaluation of the polynomial.Furthermore, due to batch technology, multiple evaluations can be turned on.KZG promises that several efficient SNARKs such as Pinocchio, Groth16, and Plonk provide the basic building blocks.It is also EIP-4844[13]the core of.For an intuitive understanding of batch processing technology, you can see our About Mina-Ethereum Bridge[14]Articles.
Practical SNARKs using elliptic curves
The first practical SNARKs constructs emerged in 2013.These configurations require preprocessing steps to generate proof and verification keys and are program/circuit specific.These keys can be quite large and depend on unknown secret parameters that should be kept; otherwise, they can forge proofs.Converting code to proveable content requires compiling the code into a series of polynomial constraint systems.At first, this has to be done manually, which is time-consuming and error-prone.Progress in this area attempts to eliminate some of the major problems:
-
There are more efficient provers.
-
Reduce the number of pretreatments.
-
Settings with general rather than specific circuits.
-
Avoid trust settings.
-
Develop methods to describe circuits in high-level languages, rather than writing polynomial constraints manually.
Pinocchio (2013)
Pinocchio[15]is the first practical, usable zk-SNARK.SNARK is based on a quadratic arithmetic program (QAP).The proof size is initially 288 bytes.Pinocchio’s toolchain provides a compiler from C code to arithmetic circuits, further converted to QAP.The protocol requires the verifier to generate keys that are circuit-specific.It uses elliptic curve pairing to check the equation.Prove that the asymptoticity of the generation and key settings is linearly related to the calculation size, and the verification time is linearly related to the size of the common input and output.
Groth 16 (2016)
Groth[16]A new knowledge argument with enhanced performance has been introduced[17], used to describe the problem of R1CS.It has the smallest proof size (only three group elements) and fast validation, involving three pairings.It also involves a preprocessing step to obtain a structured reference string.The main drawback is that it requires different trust settings for each program we want to prove, which is inconvenient.Groth16 is used by ZCash.
Bulletproofs & IPA (2016)
One weakness of KZG PCS is that it requires a trust setting.Bootle et al.[18]An effective zero-knowledge argumentation system that satisfies the internal product relationship is introduced.The inner product argument has linear prover, logarithmic communication and interaction, but linear time verification.They also developed a polynomial commitment scheme that does not require trust settings.Polynomial Commitment Scheme (PCS) using these ideas was used by Halo 2 and Kimchi.
Sonic, Marlin, and Plonk (2019)
Sonic[19], Plonk[20]and Marlin[twenty one]Addresses the issue where every program we encounter in Groth16 requires trust settings by introducing common and updating structured reference strings.Marlin provides a proof system based on R1CS (Rank-1 Constraint System) that is at the heart of Aleo.
Plonk[twenty two]A new arithmetic scheme (later called Plonkish) was introduced and a grand-product check was used to check for replication constraints.Plonkish also allows the introduction of specialized doors for certain operations, so-called custom doors.Several projects have customized versions of Plonk, including Aztec, ZK-Sync, Polygon ZKEVM, Mina’s Kimchi, Plonky2, Halo 2 and Scroll, among others.
Lookups (2018/2020)
Gabizon and Williamson introduce plookup in 2020[twenty three], use macro product checks to prove that a value is contained in a pre-calculated value table.Although the search parameters were previously in Arya[twenty four]However, this construction requires determining the multiplicity of the lookup, which makes the construction inefficient enough.PlonkUp[25]The paper shows how to introduce plookup parameters into Plonk.The problem with these lookup parameters is that they force the prover to pay for the entire table without regard to the number of lookups.This means that the cost of large tables is quite large, and people have put in a lot of effort to reduce the cost of the prover paying only the number of lookups he uses.Haböck introduces LogUp[26], which converts the grand-product check to the sum of the inverse using a log derivative.LogUp for Polygon ZKEVM[27]Performance in them is critical, they need to split the entire table into several STARK modules.These modules must be correctly linked, cross-table lookup enforces this.Introducing LogUp-GKR[28]Use the GKR protocol to improve the performance of LogUp.Caulk[29]is the first scheme to prove the time sublinear with table size, using preprocessing time O(NlogN) and storage O(N), where N is the table size.Several other options followed, such as Baloo[30], flookup[31], cq[32]and caulk+[33].Lasso[34]Several improvements are proposed to avoid committing a table when it has a given structure.Additionally, Lasso’s prover pays only for table entries accessed by the lookup operation.Jolt[35]Use Lasso to prove the execution of the virtual machine through lookups.
Spartan (2019)
Spartan[36]An IOP (“Interactive Oracle Proof.”) is provided for the circuit described using R1CS, utilizing the properties of multivariate polynomials and the sumcheck protocol.Using a suitable polynomial commitment scheme, it produces a linear time proof transparent SNARK.
HyperPlonk (2022)
HyperPlonk[37]Based on the idea of Plonk, multivariate polynomials are used.It relies on the sumcheck protocol rather than the quotient to check the execution of the constraints.It also supports high order constraints without affecting the runtime of the prover.Since it relies on multivariate polynomials, there is no need to perform FFT, and the run time of the prover is linearly related to the circuit size.HyperPlonk introduces a new permutation IOP for smaller fields, and a sumcheck-based batch opening protocol that reduces prover’s work, proof size, and validator time.
Folding schemes (2008/2021)
Nova[38]The concept of a folding scheme is introduced, which is a new method to implement incrementally verifiable computing.The concept of IVC can be traced back to Valiant[39],He shows how to combine two proofs of length k into a single proof of length k.The idea is that we can prove that the execution from step i to step I +1 is correct by recursively proof that the transformation from step i−1 to step i is correct,Any long-running calculation.Nova handles unified computing well; it is then extended to handle different types of circuits, introducing Supernova[40].Nova uses a relaxed version of R1CS and works on friendly elliptic curves.IVC is implemented using curve-friendly loops (such as Pasta curves) and is also used as the main building block for the implementation of concise state of Pickles, Mina.However, the concept of folding is different from recursive SNARK verification.
The idea of accumulator is more deeply connected to the concept of batch proof.Halo[41]The concept of accumulation is introduced as an alternative to recursive proof combinations.Protostar[42]Provides a non-uniform IVC solution for Plonk, supporting high-order gates and vector lookups.
Using anti-collision hash function
While Pinocchio was developing, there were some ideas to generate circuit/arithmetic schemes that could prove the execution of virtual machines correctly.Even though arithmetic of developing virtual machines may be more complex or less efficient than writing dedicated circuits for some programs, its advantage is that it can prove any complex program by demonstrating that the program is executed correctly in the virtual machine.The idea in TinyRAM is then improved through the design of Cairo vm, and subsequent virtual machines such as zk-evms or general purpose zkvms.Using a collision-resistant hash function eliminates the need for trusted settings or elliptic curve operations, but at the cost of proof getting longer.
TinyRAM (2013)
In SNARKs for C[43]In this article, they developed a PCP-based SNARK to prove the execution correctness of the C program, which is compiled into TinyRAM, which is a thin instruction set computer.
Note: PCP, Probabilistically Checkable Proof Probability. Verifiers can check the validity of the proof with a high confidence by reading a small part of the randomly selected content in the proof.Unlike traditional proof systems where verifiers need to check the entire proof, PCP requires only limited randomness to enable efficient verification.
The computer adopts a Harvard structure with a random memory that is addressable at byte level.Using nondeterminism, the size of the circuit is almost linearly related to the calculated size, and any data-related loops, control flows and memory access can be efficiently handled.
STARKs (2018)
STARKs[44]proposed in 2018 by Ben Sasson et al.They implement proof sizes of 0 (log^2 n), have fast prover and validator, do not require a trusted setup, and are hypothesized to be post-quantum security.They are used by Starkware/Starknet for the first time, along with Cairo vm.Its key introductions include Algebraic Intermediate Representation (AIR) and FRI protocols[45](Fast Reed-Solomon Interactive Oracle Proof of Proximity).It is also used by other projects (Polygon Miden, Risc0, Winterfell, Neptune), or has seen some adaptations of components (Boojum, Plonky2, Starky of ZK-Sync).
Ligero (2017)
Ligero[46]A proof system is proposed to implement a proof size of O(√n) , where n is the size of the circuit.It arranges polynomial coefficients into matrix form and uses linear codes.Brakedown[47]Building on Ligero, the concept of domain-independent polynomial commitment schemes was introduced.
Some new developments
The use of different proof systems in production demonstrates the advantages of each method and drives new developments.For example, plonkish arithmetic provides an easy way to include custom gates and lookup arguments; FRI has shown excellent performance as PCS, leading to Plonky.Similarly, the use of macroproduct checking in AIR (randomized AIR that brings preprocessing) improves its performance and simplifies memory access parameters.The promise of hash functions has become popular because of its speed in hardware or the introduction of new hash functions for SNARK.
New Polynomial Commitment Plan (2023)
With the emergence of efficient SNARKs based on multivariate polynomials, such as Spartan or HyperPlonk, there has been greater interest in new commitment schemes that apply to such polynomials.Binius[48]Zeromorph[49]and Basefold[50]All propose new forms of commitment to multilinear polynomials.Binius has the advantage of not having extra overhead when denoting data types (while many proof systems use at least 32-bit field elements to represent single bits) and can work on binary domains.The commitment scheme uses a brakedown designed for field-independent purposes.Basefold promotes FRI to codes other than Reed-Solomon, bringing a domain-independent PCS.
Note Domain-independent: In a domain-independent polynomial commitment scheme, the commitment process does not depend on specific properties of any particular domain.This means that commitments can be made to polynomials of any algebraic structure, such as finite domains, elliptic curves, and even integer rings.
Customizable constraint system (2023)
CCS[51]Generalized R1CS, while capturing R1CS, Plonkish and AIR arithmetics, without additional overhead.Using CCS in conjunction with Spartan IOP produces SuperSpartan, which supports high-dimensional constraints and provers do not have to bear the cryptographic cost that scales as constraint metrics increase.In particular, SuperSpartan provides AIR with a linear time proof SNARK.
in conclusion
This article describes the progress of SNARKs since the mid-1980s.Advances in computer science, mathematics and hardware, and the introduction of blockchain, have led to the emergence of new and more efficient SNARKs, opening the door to many applications that may change our society.Researchers and engineers proposed improvements and adaptations to SNARKs based on their needs, focusing on proof size, memory usage, transparent settings, post-quantum security, proof time and verification time.Although there were initially two main lines (SNARKs vs STARKs), the boundaries between the two have begun to disappear, attempting to combine the advantages of different proof systems.For example, a combination of different arithmetic schemes with new polynomial commitment schemes.We can expect that new proof systems will continue to emerge and performance will improve, and it will be difficult for some systems that take some time to adapt to keep up with these developments unless we can easily use these tools without changingSome core infrastructure.
References
[1] Link: https://blog.lambdaclass.com/our-highly-subjective-view-on-the-history-of-zero-knowledge-proofs/
[2] Link translation plan: https://github.com/lbc-team/Pioneer
[3] Translation team: https://learnblockchain.cn/people/412
[4]Tiny Bear: https://learnblockchain.cn/people/15
[5] learnblockchain.cn/article…: https://learnblockchain.cn/article/7422
[6]Article: https://blog.lambdaclass.com/transforming-the-future-with-zero-knowledge-proofs-fully-homomorphic-encryption-and-new-distributed-systems-algorithms/
[7] The Cambrian outbreak of encryption proof: https://medium.com/starkware/cambrian-explosion-of-cryptographic-proofs-5740a41cdbd2?ref=blog.lambdaclass.com
[8]The following video: https://www.youtube.com/watch?v=uchjTIlPzFo&ref=blog.lambdaclass.com
[9]sumcheck protocol: https://blog.lambdaclass.com/have-you-checked-your-sums/
[10]Lund, Fortnow, Karloff, and Nisan: https://dl.acm.org/doi/pdf/10.1145/146585.146605?ref=blog.lambdaclass.com
[11]GKR protocol: https://www.microsoft.com/en-us/research/wp-content/uploads/2016/12/2008-DelegatingComputation.pdf?ref=blog.lambdaclass.com
[12]Kate, Zaverucha, and Goldberg: https://www.iacr.org/archive/asiacrypt2010/6477178/6477178.pdf?ref=blog.lambdaclass.com
[13]EIP-4844: https://github.com/ethereum/EIPs/blob/master/EIPS/eip-4844.md?ref=blog.lambdaclass.com
[14]Mina-Ethereum Bridge: https://blog.lambdaclass.com/mina-to-ethereum-bridge/
[15]Pinocchio: https://eprint.iacr.org/2013/279?ref=blog.lambdaclass.com
[16]Groth: https://eprint.iacr.org/2016/260.pdf?ref=blog.lambdaclass.com
[17] New knowledge argument with enhanced performance: https://blog.lambdaclass.com/groth16/
[18]Bootle et al.: https://eprint.iacr.org/2016/263?ref=blog.lambdaclass.com
[19]Sonic: https://eprint.iacr.org/2019/099?ref=blog.lambdaclass.com
[20]Plonk: https://eprint.iacr.org/2019/953?ref=blog.lambdaclass.com
[21]Marlin: https://eprint.iacr.org/2019/1047?ref=blog.lambdaclass.com
[22]Plonk: https://blog.lambdaclass.com/all-you-wanted-to-know-about-plonk/
[23]plookup: https://eprint.iacr.org/2020/315?ref=blog.lambdaclass.com
[24]Arya: https://eprint.iacr.org/2018/380?ref=blog.lambdaclass.com
[25]PlonkUp: https://eprint.iacr.org/2022/086?ref=blog.lambdaclass.com
[26]LogUp: https://eprint.iacr.org/2022/1530?ref=blog.lambdaclass.com
[27]Polygon ZKEVM: https://toposware.medium.com/beyond-limits-pushing-the-boundaries-of-zk-evm-9dd0c5ec9fca?ref=blog.lambdaclass.com
[28]LogUp-GKR: https://eprint.iacr.org/2023/1284?ref=blog.lambdaclass.com
[29]Caulk: https://eprint.iacr.org/2022/621?ref=blog.lambdaclass.com
[30]Baloo: https://eprint.iacr.org/2022/1565?ref=blog.lambdaclass.com
[31]flookup: https://eprint.iacr.org/2022/1447?ref=blog.lambdaclass.com
[32]cq: https://eprint.iacr.org/2022/1763?ref=blog.lambdaclass.com
[33]caulk+: https://eprint.iacr.org/2022/957?ref=blog.lambdaclass.com
[34]Lasso: https://eprint.iacr.org/2023/1216?ref=blog.lambdaclass.com
[35]Jolt: https://eprint.iacr.org/2023/1217?ref=blog.lambdaclass.com
[36]Spartan: https://eprint.iacr.org/2019/550?ref=blog.lambdaclass.com
[37]HyperPlonk: https://eprint.iacr.org/2022/1355.pdf?ref=blog.lambdaclass.com
[38]Nova: https://eprint.iacr.org/2021/370?ref=blog.lambdaclass.com
[39]Valiant: https://https//iacr.org/archive/tcc2008/49480001/49480001.pdf?ref=blog.lambdaclass.com
[40]Supernova: https://eprint.iacr.org/2022/1758?ref=blog.lambdaclass.com
[41]Halo: https://eprint.iacr.org/2019/1021.pdf?ref=blog.lambdaclass.com
[42]Protostar: https://eprint.iacr.org/2023/620?ref=blog.lambdaclass.com
[43]SNARKs for C: https://eprint.iacr.org/2013/507?ref=blog.lambdaclass.com
[44]STARKs: https://eprint.iacr.org/2018/046?ref=blog.lambdaclass.com
[45]FRI protocol: https://blog.lambdaclass.com/how-to-code-fri-from-scratch/
[46]Ligero: https://eprint.iacr.org/2022/1608?ref=blog.lambdaclass.com
[47]Brakedown: https://eprint.iacr.org/2021/1043?ref=blog.lambdaclass.com
[48]Binius: https://blog.lambdaclass.com/snarks-on-binary-fields-binius/
[49]Zeromorph: https://eprint.iacr.org/2023/917?ref=blog.lambdaclass.com
[50]Basefold: https://blog.lambdaclass.com/how-does-basefold-polynomial-commitment-scheme-generalize-fri/
[51]CCS: https://eprint.iacr.org/2023/552?ref=blog.lambdaclass.com
[52]DeCert.me: https://decert.me/