
作者:0xTodd 來源:X,@0x_Todd
最近行情不佳,終於時間充裕了一些,可以繼續分亨一些新的技術路線。儘管2024年的加密市場不如過去那樣波瀾壯闊,但依然有一些新的技術試著走向成熟,比如說我們今天要聊的主題:「 FHE/全同態加密(FullyHomomorphic Encryption) 」。
V神在今年 5月也專門發表了一篇關於 FHE 的文章,推薦感興趣的朋友們說讀。
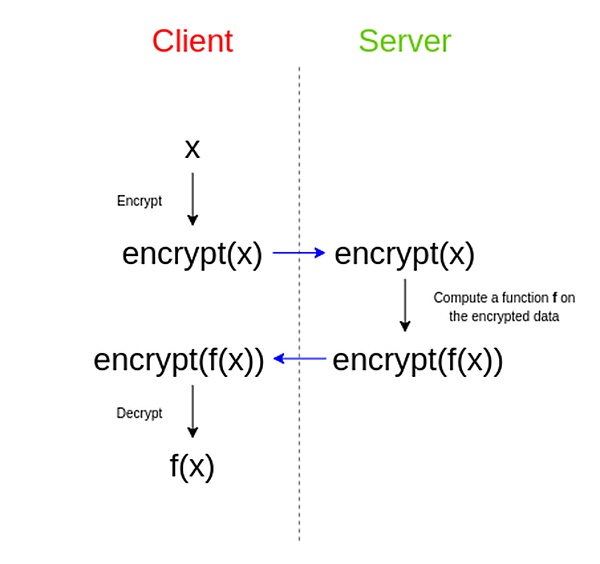
那麼 FHE 到底是一門什麼技術?
想要理解 FHE全同態加密 這個拗口的名詞,必須先理解什麼是 「加密」 ,什麼是 「同態」 ,以及為什麼要「全」。
一、 什麼是加密?
普通的加密大家最熟悉。舉個例子,Alice 要發個口信給 Bob,比如要發個「1314 520」。
如果現在,既要第三方C來送信,又要做到信息保密,那麼很簡單——只需要將每個數字 x2 來加密,比如變成「2628 1040」即可。
當 Bob 收到後,將每個數字依次除 2,就解密出了原來 Alice 在說「1314 520」
看到了麼,兩人通過對稱加密,在既要僱C出力卻又要 C不知道信息的情況下,完成了信息傳遞。一般,諜戰片裡,兩個聯絡員相互通信大抵不會超過這個範疇。

二、那什麼是同態加密呢?
現在 Alice 的需求難度升級了:
比如 Alice 只有7歲;
Alice 只會算 x2 和 ÷2 這樣最簡單的算術,其他運算則一概不懂。
好,那現在假設 Alice 要交電費了,Alice 家每月電費是 400 元,一共拖欠了 12 個月。
然而,400*12=幾,這道題目超過了年僅7歲的Alice 的計算範圍,她不會這麼複雜的計算,
但是,她不想讓別人知道她家電費多少錢/幾個月,因為這是敏感信息。
因此,Alice 在不信任C的情況下,拜託C來幫忙計算。
因為她只會 x2 -2,因此她使用 x2 乘法給她的數字做了簡單的加密,於是,她告訴C,讓C計算800×24=多少,即:(400×2)乘(12×2)。
C是成年人, 擁有強大的計算腦力 ,很快就口算出了800*24=19200,並且把數字告訴了Aice。然後,Alice 將結果,也就是19200÷2÷2,很快就知道原來自己要繳納 4800 元水費。
看到了麼?這就是最簡單的一個乘法同態加密,800*24 只是 400*12 的映射,變幻前後實際上形態是相同的,因此稱之為「同態」。
這樣的加密方式實現了: 某人要委託一個不信任的實體計算結果,卻能保證自己的敏感數字不洩露。

三、那為什麼「同態加密」還要「全」呢?
但是,剛剛只是理想世界裡的問題,現實世界上的問題並沒有這麼簡單,不是所有人都是7歲,或者都像 C 那麼老實。
我們假設一種很壞的情況,比如C可能會嘗試反推,C通過窮舉法也能破譯出Alice要計算的是 400和 12。
這時候,就需要「全同態加密」來解決。
Alice 給每個數字都x2,這個2可以視作一個噪聲。噪聲太少,就容易被 C破解。
所以,Alice 可以在乘法基礎上,再引入一道加法。
當然,最好這個噪聲猶如早九點的主幹道十字路口,那麼C的破解難度就比登天還難。
所以,Alice 可以再乘 4次,加8次,這樣C破解概率就大幅降低了
然而,這樣 Alice 仍然只是「部分」同態加密,即:
(1)她加密內容只能針對特定部分問題;
(2)她只能使用特定部分運算法則,因為加法乘法次數不可太多(一般不能超過 15 次)
而「全」的意思是說,要允許 Alice 針對一個多項式,能夠做加法加密任意次,做乘法加密任意次,這樣委託第三方完全計算,解密後還能得到正確結果。
一個超級長的多項式,幾乎可以表達世界上絕大部分的數學問題,而不僅僅計算電費這種7歲小朋友的問題。
再加套上了任意次的加密, 從根本上就幾乎杜絕了C想要窺探隱私數據的可能性,真正實現了「既要又要」。
因此,「全同態加密」這門技術,一直是加密學聖杯上的一顆明珠。
事實上,同態加密這門技術一直到 2009 年之前,都只支持「部分同態加密」。
而 2009 年 Gentry 等學者提出的新思路,才打開了全同態加密可能性的大門。感興趣的讀者也可以移步這篇論文。

很多朋友對這門技術的應用場景,仍然抱有疑惑,什麼場景會需要使用全同態加密(FHE)技術呢?
比如說——AI。
大家都知道,一個強悍的 AI需要足夠多的數據餵養,但偏偏很多數據的隱私價值又太高。那麼能不能通過 FHE 實現這個問題的「既要又要」呢?
答案是可以的
你可以:
(1)把你的敏感數據按照 FHE方式進行加密;
(2)用加密後的數據交給AI計算;
(3)然後 AI給你吐出一坨誰也看不懂的亂碼。
非監督 AI可以實現這一點,因為這些數據在它那裡本質就是向量,AI 尤其是 GPT這類生成型AI,壓根就不理解我們給它輸入的話,只不過它通過向量「預測」出了最應該回答的話。
然而,由於這坨亂碼遵循著某種數學規則,而你正是加密它的主人,那麼:
(4)你大可以斷開網絡,在本地從容解密這些亂碼,就像 Alice 一樣;
(5)進而,你實現了: 讓AI 對你的敏感數據完全不經手的條件下,運用龐大算力幫你完成了計算。
而現在的 AI則做不到這點,必須放棄隱私才行,想想你明文輸入給 GPT的一切吧!要實現這個,非FHE 不可。
這就是 AI和 FHE 天生契合的根源,千言萬語化成個詞:既要又要。
由於 FHE 和 AI掛上了鉤,橫跨加密和 AI 兩大領域,自然得到了額外的青睞,關於FHE的項目不少,比如Zama, Privasea, Mind Network, Fhenix,Sunscreen 等等,FHE應用的方向也各有創意。
今天拿其中一個項目 @Privasea_ai出來做個解析。
這是個幣安領投的 FHE項目,它的白皮書描述了個很貼切的場景,比如說人臉識別。
既要:機器算力能夠判斷此人是否為真人;
又要:機器不經手任何人臉敏感信息。
引入 FHE,能夠有效解決這個難題
然而,如果真要做現實世界的 FHE計算,需要非常龐大的算力,畢竟 Alice 要做「任意次」的加法和乘法加密,無論是計算,加密、解密都是一個頗耗算力的過程。
因此,在 Privasea 要組建一個強大的算力網絡,以及配套設施。因此,Privasea又提出了一個類PoW+類 PoS 網絡的架構來解決這個算力網絡的問題。
最近,Privasea剛剛宣布了自己的 PoW 硬體,叫做WorkHeart USB,這個可以理解為是 Privasea 的算力網絡的配套設施之一,當然你可以簡單理解它為一個礦機。
初始定價是 0.2 ETH,能夠挖出網絡的 6.66%總代中。
以及還有一個類 PoS 資產,叫做 StarFuel NFT,這個可以理解為「工作證」,總量 5000個。
初始定價也是 0.2 ETH,能夠領到網絡的 0.75%總代幣(通過空投)。
這個 NFT 也有點意思,它是類 PoS,但不是真PoS, 它在試圖迴避「PoS 在美國到底是不是證券」的問題。
這個 NFT 支持用戶往裡面抵押 Privasea 的代幣,但是它不直接產生 PoS 收益,而是讓你綁定的 USB 設備挖礦效率加倍,所以是個變相 PoS。
PS:之前投了這個項目,所以我有一個打折 mint 早鳥邀請碼 siA7PO 感興趣請自取
nft.privasea.ai/
書歸正傳,如果AI 真的能夠大規模普及 FHE 技術,那麼對於 AI 自己來說真的是個福音,要知道現在很多國家監管A的重點都在數據安全和數據隱私。
甚至,舉個不恰當的例子,比如俄烏戰爭裡,一些俄國軍方都在試圖使用A,但是考慮到大量AI公司的美國背景,大概情報部門要被穿透得千瘡百孔了。
但是如果不使用 AI,又自然會落後一大截。哪怕現在可能差距還不大,再給10年時間,也許我們都無法想像沒有 AI的世界了。
因此,數據隱私,大到兩國戰爭衝突,小到手機人臉解鎖,無處無存在於我們的生活。
而 AI的時代,如果 FHE 技術能夠真正成熟,那無疑是人類的最後一道防線。







